- 平面向量的概念及线性运算、平面向量基本定理
- 共611题
13.设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m= .
正确答案
解析
试题分析：由
考查方向
解题思路
先根据|a+b|2=|a|2+|b|2 求出
易错点
相关知识点不熟悉导致出错。
知识点
3.已知向量
正确答案
知识点
3.在平面直角坐标系xOy中，双曲线
正确答案
知识点
22．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分
已知
(1) 当
(2) 若关于
(3) 设
正确答案
(1)
∴不等式的解为
(2)依题意，
∴
可得
即
当
当
当
若
若
要使得方程①有且仅有一个解，则
综上，若原方程的解集有且只有一个元素，则
(3)
依题意，
即
∴
设
当
当
∵函数
∴
∴
∴
知识点
15.已知向量a，b，|a|=1，|b|=2，若对任意单位向量e，均有|a·e|+|b·e|
正确答案
解析
考查方向
解题思路
利用极化不等式
易错点
对向量e任意性的理解。
知识点
5．设
A若
B若
C
D若
正确答案
解析
如图，为矩形.
设
两条平行直线，其中一条垂直一个平面，那么另一条也垂直于这个平面，故B正确；
对于C，设
对于D,设
知识点
8．称
①
②
③对任意的
则（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16.已知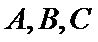
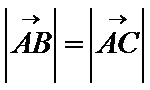
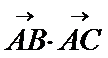
正确答案
解析
1.设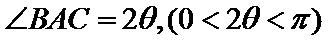
则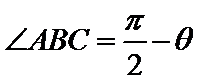
则
所以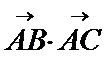
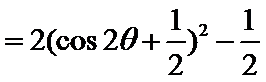
所以当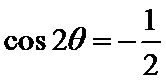
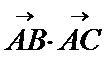
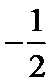
考查方向
易错点
1.不能正确引入变量表示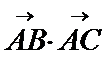
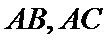
知识点
16. 设
A充分不必要条件
B
C充要条件
D既不充分也不必要条件
正确答案
解析
由余弦函数的单调性可知
因为
所以“
考查方向
解题思路
本题考查平面向量的基础知识，直接运算即可。把条件判断转化为集合关系的判断更有利于解题。
易错点
本题必须注意充要条件的判定的方向性，A是B的XX条件和A的XX条件是B要区分清楚，忽视则会出现错误。
知识点
扫码查看完整答案与解析