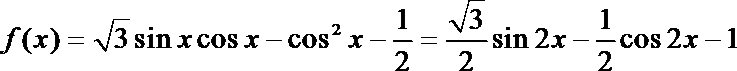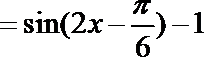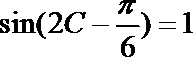- 平面向量的概念及线性运算、平面向量基本定理
- 共611题
20.若a,b是两个不共线的非零向量,t∈R.
(1)若a,b起点相同,t为何值时,a,tb,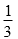
(2)若|a|=|b|,且a与b夹角为60°,t为何值时,|a-tb|的值最小?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知向量
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.已知向量a=(4,2),b=(x,3),且a∥b,则x的值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,角A,B,C的对边分别为a,b,c.设向量

(1)若

(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知

(1)求函数
(2)若在锐角



正确答案
(1) 

(2) 由(1)及

∵ 
∴ A=60°.
由余弦定理得3=b2+c2-2bccos60°,即(b+c)2=3+bc,
∴ (b+c)2=3+bc≤3+
所以,△ABC周长最大值为
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数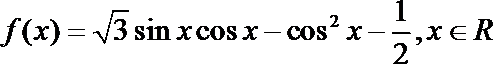
(1) 求函数
(2)已知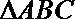
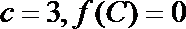
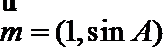
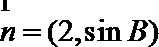
正确答案
(1)
∴ 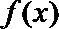
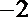


(2)∵ 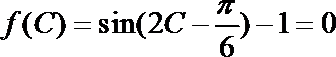
∵ 
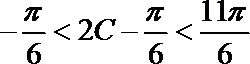

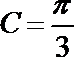
∵ 
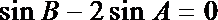
由正弦定理 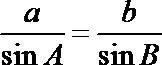
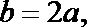
∵ 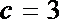
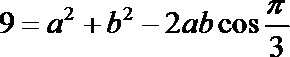
解方程组①②,得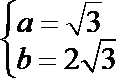
解析
解析已在路上飞奔,马上就到!
知识点
16.在


(1)求角B的大小;
(2)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在



(1)求角B的大小;
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)判断函数

(Ⅱ)求函数
(Ⅲ)如果关于x的方程
正确答案
(Ⅰ)设

∴

(Ⅱ)当




当






(Ⅲ)当x=0时,
当x>0时,

当x<0时,

即看函数
与函数

∴
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析