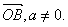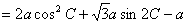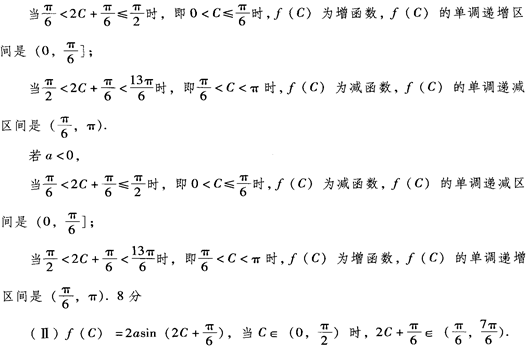- 平面向量的概念及线性运算、平面向量基本定理
- 共611题
设向量


已知向量






正确答案
解析
略
知识点
已知



正确答案
解析
:由题意知 λ

又因为两向量垂直,
所以(-3λ﹣1,2λ)(﹣1,2)=0,即3λ+1+4λ=0,
解得λ=
故选A。
知识点
已知函数

(1)求
(2)求
(3)若


正确答案
见解析。
解析
(1)
(2)由

又

∵


∴
(3)由(2)得
即

∵
∴
∴
知识点
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)




①两点列的起点和终点分别相同;②线段

则称

(1)求


(2)判断


(3)

正确答案
见解析
解析
(1)设点列

由正交点列的定义可知



由正交点列的定义可知 

即
所以点列

(2)由题可得 
设点列

则可设
因为
因为
所以有序整点列
(3)




若有序整点列

则
则有
①当

由于


等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列
②当
取

由于


等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列
综上所述,

知识点
已知向量


正确答案
解析
略
知识点
在平面直角坐标系中,已知动点







(1)求动点

(2)设直线




(3)若直线










正确答案
见解析
解析
(1)依据题意,可得点

又




(2) 若直线



设直线


由

设点



又
于是,

解得
所以,所求直线
证明(3)








由(2)可得点
可算得
又直线
设点









知识点
在△ABC中,向量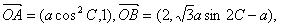
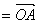
(1)求函数f(C)解析式,并求f(C)的单调区间;
(2)若△ABC是锐角三角形时,当a>O时,f(C)的最大值为5,求a的值。
正确答案
见解析。
解析
(1) f(C)
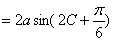
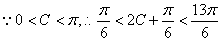
若a>O,
知识点
已知向量



正确答案
解析
略
知识点
设


正确答案
解析
略
知识点
已知平面向量




正确答案
解析
略
知识点
扫码查看完整答案与解析