平面向量的概念及线性运算、平面向量基本定理
共611题

平面向量的概念及线性运算、平面向量基本定理
共611题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

9．已知，若点是所在平面内一点，且，则的最大值等于（）

A13

B15

C19

D21

正确答案

解析

以为坐标原点，建立平面直角坐标系，如图所示，则，，，即，所以，，因此

，因为，所以的最大值等于，当，即时取等号．

考查方向

1、平面向量数量积；2、基本不等式．

解题思路

建系，由向量的几何意义得到P的坐标，然后利用基本不等式求得。

易错点

计算能力弱，数量积转换坐标时错误

知识点

向量的减法及其几何意义

题型：填空题

填空题 · 4 分

15.已知向量a，b，|a|=1，|b|=2，若对任意单位向量e，均有|a·e|+|b·e|，则a·b的最大值是 .

正确答案

知识点

向量的减法及其几何意义

题型：填空题

填空题 · 6 分

如图，在中，AB=BC=2，.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是.

正确答案

知识点

向量的减法及其几何意义

题型：单选题

单选题 · 5 分

6.在平行四边形ABCD中，，点分别在边上，且，则=（）

正确答案

解析

,,所以，故选C选项。

考查方向

本题主要考查向量的线性运算和向量的数量积运算等知识，意在考查考生的运算求解能力和数形结合能力。

解题思路

1.先将向量,用基底表示出来；2.后利用数量积的运算法则求解即可。

易错点

不知道应该将向量,用基底表示出来；2.运算出错。

知识点

向量的几何表示向量的减法及其几何意义

题型：填空题

填空题 · 5 分

12．在边长为1的正三角形ABC中，设=2，=3，则·=__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量数乘的运算及其几何意义平面向量数量积的运算

题型：单选题

单选题 · 4 分

13. 过的重心任作一直线分别交、于点、，若则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量数乘的运算及其几何意义向量在几何中的应用

题型：简答题

简答题 · 12 分

20．若a，b是两个不共线的非零向量，t∈R．

（1）若a，b起点相同，t为何值时，a，tb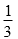，（a＋b）三向量的终点在一直线上？

（2）若|a|＝|b|，且a与b夹角为60°，t为何值时，|a－tb|的值最小？

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平行向量与共线向量两向量的和或差的模的最值数量积表示两个向量的夹角

题型：单选题

单选题 · 5 分

5.已知向量，，其中.则“”是“”成立的（）

A充分而不必要条件

B必要而不充分条件

C充要条件

D既不充分又不必要条件

正确答案

解析

此题中向量垂直的充分必要条件是，,所以由前面可以推出后面，但是由后面推不出来前面，所以是充分而不必要条件

考查方向

平面向量的数量积，向量垂直，充分条件与必要条件

解题思路

根据向量垂直数量积的特点进行求解

易错点

充分条件和必要条件理解错误，向量垂直推出的结论

知识点

向量的减法及其几何意义

题型：填空题

填空题 · 5 分

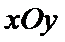
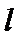
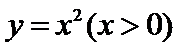
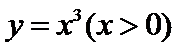
13．阿在平面直角坐标系中，直线与曲线和均相切，

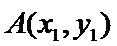
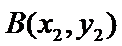
切点分别为和,则的值是_________

正确答案

解析

由题设函数y＝x2在A(x1，y1)处的切线方程为：y＝2x1 x－x12，

函数y＝x3在B(x2，y2)处的切线方程为y＝3 x22 x－2x23．

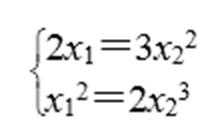
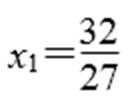
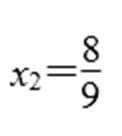
所以，解之得：，．

所以．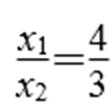

考查方向

本题主要考查导数的概念，函数的切线方程．考查运算能力，推理论证能力及灵活运用数学知识能力，难度中等.

解题思路

本题主要考查导数的概念，函数的切线方程．

解题步骤如下：由导数几何意义，写出切线方程。解方程组，得出答案。

易错点

本题易错的地方是不能正确理解导数的几何意义，以及导数公式记错。

知识点

向量的减法及其几何意义

题型：简答题

多选题

房地产价格构成的基本要素有( )。

A．土地价格
B．税金
C．利润
D．租金收入
E．房屋建筑成本

正确答案

A,B,C,E

解析

[解析] 房地产价格构成的基本要素有土地价格或使用费、房屋建筑成本、税金和利润等。

继续学习学习下一知识点

下一知识点 : 平面向量的数量积及其应用

百度题库 > 高考 > 理科数学 > 平面向量的概念及线性运算、平面向量基本定理

扫码查看完整答案与解析