- 平面向量的概念及线性运算、平面向量基本定理
- 共611题
11.在等腰直角
若
A
B
C
D
正确答案
解析
∵
∴A，B，D三点共线，
∴由题意建立如图所示坐标系，
设AC=BC=1，则C(0，0)，A(1，0)，B(0，1)，
直线AB的方程为
直线CD的方程为
故联立解得，
故
故
故
故
故选A.
考查方向
解题思路
易知A，B，D三点共线，从而建立坐标系，从而利用坐标运算求解即可．
易错点
在平面中A、B、C三点共线的充要条件是： 
知识点
6.设
A
B
C
D
正确答案
解析
以
∴
∴
考查方向
解题思路
该题属于常规题1、把
易错点
主要易错不能有效理解BCD的关系
知识点
P是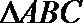
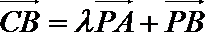
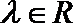
A
BAC边所在直线上
CAB边所在直线上
DBC边所在直线上
正确答案
解析
由已知，得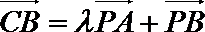
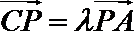
考查方向
本题主要考查了向量的基本运算以及平面几何的综合应用
易错点
向量基本运算需要仔细运算
知识点
4. 在
A
B
C
D
正确答案
解析
由
所以，
考查方向
本题考查了向量的线性运算及三角形法则等知识。
解题思路
由
易错点
向量的三角形法则不能熟练掌握，导致运算错误。
知识点
16.在平面直角坐标系中，设
正确答案
解析
因为
即是
画出可行域如图
又因为，
上式可看成是点（a,b）与点(0,-1)距离的平方和加上点（a,b）与点(0,-1)连线的斜率再减掉1，由图可知，在点（1，0）处它们同时取得最小值，代入可得最小值为2，即取值范围为
考查方向
本题是解析几何，向量，线性规划的高难度综合题，属于难题。
解题思路
（1）作出点(a,b)的可行域。
（2）找出式子
易错点
（1） 易忽视“点
（2）对向量
（3）对
知识点
6．如图，在△OAB中，点P在边AB上，且AP：PB=3：2．则
A
B
C
D
正确答案
考查方向
易错点
1、本题在AP：PB=3：2变换成
知识点
3．如图，正方形
A
B
C
D
正确答案
解析
考查方向
本题主要考察了平面向量的基本定理，属于中档题，是高考的热点，解决此类题的关键是会利用平面向量的基本定理，用两个不共线的向量表示平面内任一向量。
易错点
本题易在向量的表示过程中出现错误。
知识点
16．已知点A（0，－1），B（3，0），C（1，2），平面区域P是由所有满足
正确答案
解析
由题可知，设M（x,y），则
8<x≤3m+n,7<y≤m+3n-1，画出平面区域，利用面积公式可得（m+n）min=
考查方向
本题主要考查线性规划及向量的线性运算。
解题思路
1、画出平面区域
2、化简公式求解．
易错点
本题必须注意利用图像完成。
知识点
11.如图，在矩形OABC中，点E、F分别在线段AB、BC上，且满足AB=3AE，BC=3CF，若
正确答案
解析
又因为
所以
考查方向
解题思路
本题适宜于先拆分向量，把向量都用
易错点
本题必须注意向量和线段的区别，条件BC=3CF若改为向量形式，就没有
知识点
3．设
A
B
C
D
正确答案
解析
取ＡＢ中点M，则由向量加法的平行四边形法则知
考查方向
解题思路
运用数形结合的思想解决问题，通过 
易错点
不能把
知识点
扫码查看完整答案与解析