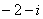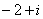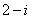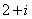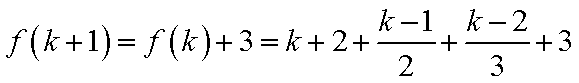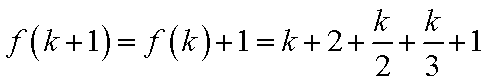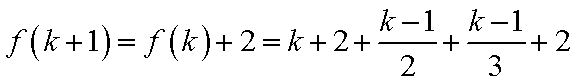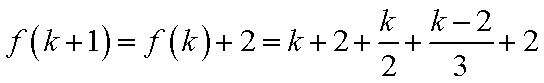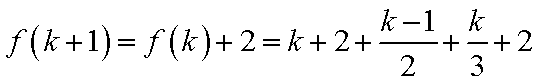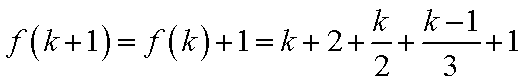- 元素与集合关系的判断
- 共59题
2.设集合
A
B
C
D
正确答案
解析
使用集合交集的性质，借助数轴容易得出答案。选A
考查方向
解题思路
本题属于简单题，可使用数轴表示出集合直接判断，
易错点
该题主要易错于对端点情况的判断错误
知识点
1.定义集合
A
B3
C4
D无数个
正确答案
解析
考查方向
解题思路
1.先根据题中给出的新定义求出
易错点
1.不理解题中给出的新定义；2.记不住子集的个数是多少个导致出错（忘记空集）
知识点
1.
A
B
C
D
正确答案
解析
奇数集合有三种表达方法
考查方向
解题思路
奇数集合有三种表达方法
易错点
奇数集合不熟
知识点
已知集合X={1，2，3}，Yn={1，2，3，…，n）（n∈N*），设Sn={（a，b）|a整除b或整除a，a∈X，B∈Yn}，令f（n）表示集合Sn所含元素的个数．
36.写出f（6）的值；
37.当n≥6时，写出f（n）的表达式，并用数学归纳法证明．
正确答案
13
解析
（1）f（6）=6+2+
考查方向
解题思路
（1）f（6）=6+2+
易错点
本题在计算时易错.
正确答案
（2）当n≥6时，f（n）=
下面用数学归纳法证明：
①n=6时，f（6）=6+2+
②假设n=k（k≥6）时，结论成立，那么n=k+1时，Sk+1在Sk的基础上新增加的元素在（1，k+1），（2，k+1），（3，k+1）中产生，分以下情形讨论：
1）若k+1=6t，则k=6（t﹣1）+5，此时有f（k+1）=f（k）+3=（k+1）+2+
2）若k+1=6t+1，则k=6t+1，此时有f（k+1）=f（k）+1=k+2+
3）若k+1=6t+2，则k=6t+1，此时有f（k+1）=f（k）+2=k+2+
4）若k+1=6t+3，则k=6t+2，此时有f（k+1）=f（k）+2=k+2+
5）若k+1=6t+4，则k=6t+3，此时有f（k+1）=f（k）+2=k+2+
6）若k+1=6t+5，则k=6t+4，此时有f（k+1）=f（k）+2=k+2+
综上所述，结论对满足n≥6的自然数n均成立．
解析
见答案
考查方向
解题思路
（2）根据数学归纳法的证明步骤，分类讨论，即可证明结论．
易错点
本题考查数学归纳法，在归纳的过程中易错.
2. 已知集合
A
B
C
D
正确答案
解析
考查方向
解题思路
化简M，N，再计算补集
易错点
集合的代表元素属性，N集合易出化为
知识点
1.已知集合
正确答案
解析
考查方向
解题思路
1.先分别将集合A,B化简；2.利用数轴求两个集合的交集。
易错点
对于集合A的理解不到位，导致理解成y的范围致错。
知识点
若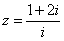
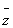
A
B
C
D
正确答案
解析
知识点
已知集合A＝{x|x2﹣x﹣6＜0}，集合B＝{x|x﹣1＞0}，则（∁RA）∩B＝（ ）
正确答案
知识点
23.已知集合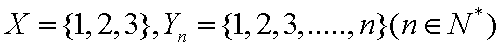
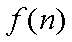
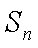
（1）写出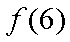
（2）当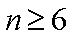
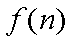
正确答案
（1）
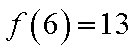
（2）当
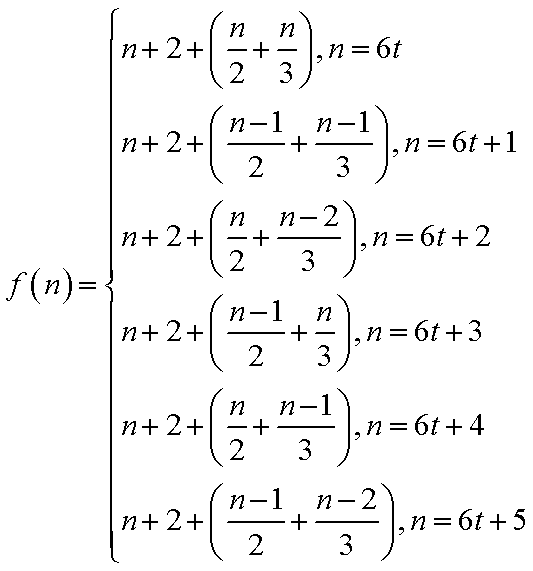
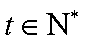
下面用数学归纳法证明：
①当
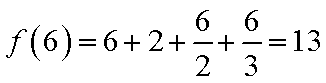
②假设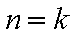
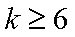
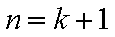
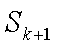
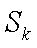
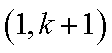
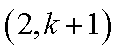
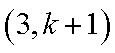
1）若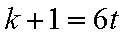
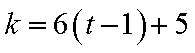
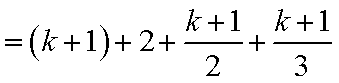
2）若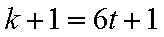
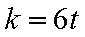
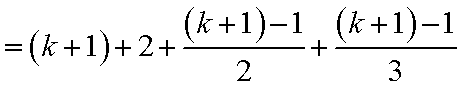
3）若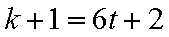
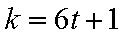
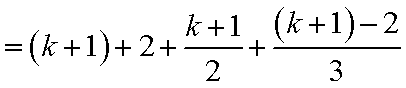
4）若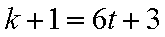
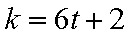
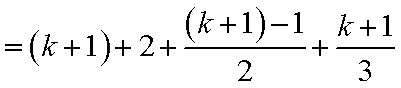
5）若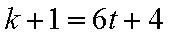
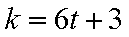
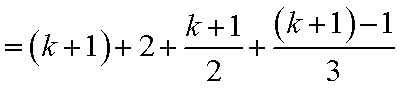
6）若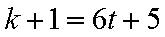
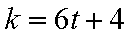
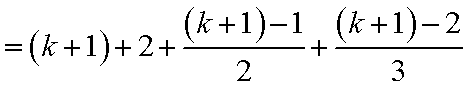
综上所述，结论对满足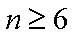
解析
解析已在路上飞奔，马上就到！
知识点
执行如图所示的程序框图，输出的
正确答案
解析
略
知识点
扫码查看完整答案与解析