带电粒子在匀强磁场中的运动_章节学习

1

题型：单选题

|

单选题 · 6 分

“人造小太阳”托卡马克装置使用强磁场约束高温等离子体，使其中的带电粒子被尽可能限制在装置内部，而不与装置器壁碰撞。已知等离子体中带电粒子的平均动能与等离子体的温度T成正比，为约束更高温度的等离子体，则需要更强的磁场，以使带电粒子的运动半径不变。由此可判断所需的磁感应强度B正比于

A

B

C

D

正确答案

A

解析

由于等离子体中带电粒子的平均动能与等离子体的温度T成正比，即。带电粒子在磁场中做圆周运动，洛仑磁力提供向心力：得。而故可得：又带电粒子的运动半径不变，所以。A正确。

知识点

带电粒子在匀强磁场中的运动

1

题型：单选题

|

单选题 · 6 分

如图所示，圆形区域内有垂直于纸面向里的匀强磁场，一个带电粒子以速度从点沿直径方向射入磁场，经过时间从点射出磁场，与成60°角。现将带电粒子的速度变为/3，仍从点沿原方向射入磁场，不计重力，则粒子在磁场中的运动时间变为

A

B2

C

D3

正确答案

B

解析

带电粒子在匀强磁场中做匀速圆周运动，由洛伦兹力提供向心力，据牛顿第二定律有，解得粒子第一次通过磁场区时的半径为，圆弧AC所对应的圆心角∠AO′C＝60°，经历的时间为（T为粒子在匀强磁场中运动周期，大小为，与粒子速度大小无关）；当粒子速度减小为v/3后，根据知其在磁场中的轨道半径变为r/3，粒子将从D点射出，根据图中几何关系得圆弧AD所对应的圆心角∠AO″D＝120°，经历的时间为，由此可知B项正确。

知识点

带电粒子在匀强磁场中的运动

1

题型：单选题

|

单选题 · 6 分

处于匀强磁场中的一个带电粒子，仅在磁场力作用下做匀速圈周运动。将该粒子的运动等效为环形电流，那么此电流值（　）

A与粒子电荷量成正比

B与粒子速率成正比

C与粒子质量成正比

D与磁感应强度成正比

正确答案

D

解析

电流的定义式：

从公式中可以看出：电流值和磁感应强度成正比，和电荷量的平方成正比，和质量成反比。所以，选择D。

知识点

电源和电流带电粒子在匀强磁场中的运动

1

题型：单选题

|

单选题 · 6 分

质量和电量都相等的带电粒子M和N，以不同的速度率经小孔S垂直进入均强磁场，运行的半圆轨迹如图2种虚线所示，下列表述正确的是

AM带负电，N带正电

BM的速度率小于N的速率

C洛伦磁力对M.N做正功

DM的运行时间大于N的运行时间

正确答案

A

解析

由左手定则知M带负电，N带正电，在由得M的速度比N大，运行时间由(为带电粒子转过的圆心角)因而选：A

知识点

运动电荷在磁场中受到的力带电粒子在匀强磁场中的运动

1

题型：简答题

|

简答题 · 18 分

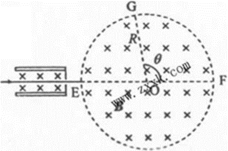
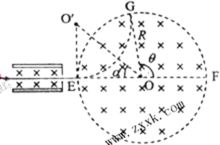
如图，一半径为R的圆表示一柱形区域的横截面（纸面）。在柱形区域内加一方向垂直于纸面的匀强磁场，一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域，在圆上的b点离开该区域，离开时速度方向与直线垂直。圆心O到直线的距离为。现将磁场换为平等于纸面且垂直于直线的匀强电场，同一粒子以同样速度沿直线在a点射入柱形区域，也在b点离开该区域。若磁感应强度大小为B，不计重力，求电场强度的大小。

正确答案

解析

粒子在磁场中做圆周运动，设圆周的半径为r，由牛顿第二定律和洛仑兹力公式得

① 式中v为粒子在a点的速度。

过b点和O点作直线的垂线，分别与直线交于c和d点。由几何关系知，线段、和过a、b两点的轨迹圆弧的两条半径围成一正方形。因此，　②

设=x，由几何关系得 ③

④

联立式得　⑤

再考虑粒子在电场中的运动。设电场强度的大小为E，粒子在电场中做类平抛运动。设其加速度大小为a，由牛顿第二定律和带电粒子在电场中受力公式得

⑥

粒子在电场方向和直线方向所走的距离均为r，由运动学公式得

⑦ vt　⑧

式中t是粒子在电场中运动的时间，联立式得 ⑨

知识点

带电粒子在匀强电场中的运动带电粒子在匀强磁场中的运动

1

题型：简答题

|

简答题 · 16 分

某装置用磁场控制带电粒子的运动，工作原理如图所示。装置的长为L，上下两个相同的矩形区域内存在匀强磁场，磁感应强度大小均为B、方向与纸面垂直且相反，两磁场的间距为d。装置右端有一收集板，M、N、P为板上的三点，M位于轴线上，N、P分别位于下方磁场的上、下边界上。在纸面内，质量为m、电荷量为-q的粒子以某一速度从装置左端的中点射入，方向与轴线成300角，经过上方的磁场区域一次，恰好到达P点。改变粒子入射速度的大小，可以控制粒子到达收集板上的位置。不计粒子的重力。

(1) 求磁场区域的宽度h；

(2)欲使粒子到达收集板的位置从P点移到N点，求粒子入射速度的最小变化量Δv；

(3)欲使粒子到达M点，求粒子入射速度大小的可能值。

正确答案

答案：（1）（2）

（3）

解析

（1）设粒子的轨道半径为r

根据题意且

解得

（2）改变入射速度后粒子在磁场中的轨道半径为

，

由题意可知解得

设粒子经过上方磁场n次

由题意可知

且解得

知识点

带电粒子在匀强磁场中的运动

1

题型：单选题

|

单选题 · 6 分

带电粒子a.b在同一匀强磁场中做匀速圆周运动，他们的动量大小相等，a运动的半径大于b运动的半径。若a.b的电荷量分别为qa.qb，质量分别为ma.mb,周期分别为Ta.Tb。则一定有

A

B

C

D

正确答案

A

解析

略

知识点

动量冲量带电粒子在匀强磁场中的运动

1

题型：单选题

|

单选题 · 6 分

如题21图所式，矩形MNPQ区域内有方向垂直于纸面的匀强磁场，有5个带点粒子从图中箭头所示位置垂直于磁场边界进入磁场，在纸面内做匀速圆周运动，运动轨迹为相应的圆弧，，这些粒子的质量，电荷量以及速度大小如下表所示。

由以上信息可知，从图中abc处进入的粒子对应表中的编号分别为

A3，5， 4

B4，2，5

C5，3，2

D2，4，5

正确答案

D

解析

根据半径公式结合表格中数据可求得1—5各组粒子的半径之比依次为0.5︰2︰3︰3︰2，说明第一组正粒子的半径最小，该粒子从MQ边界进入磁场逆时针运动。由图a、b粒子进入磁场也是逆时针运动，则都为正电荷，而且a、b粒子的半径比为2︰3，则a一定是第2组粒子，b是第4组粒子。c顺时针运动，都为负电荷，半径与a相等是第5组粒子。正确答案D

知识点

带电粒子在匀强磁场中的运动

1

题型：简答题

|

简答题 · 21 分

如下图，在区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B.在t=0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0～180°范围内。已知沿y轴正方向发射的粒子在时刻刚好从磁场边界上点离开磁场。求：

（1）粒子在磁场中做圆周运动的半径R及粒子的比荷q／m

（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围

（3）从粒子发射到全部粒子离开磁场所用的时间。

正确答案

（1）

（2）速度与y轴的正方向的夹角范围是60°到120°

（3）从粒子发射到全部离开所用时间为

解析

（1）粒子沿y轴的正方向进入磁场，从P点经过做OP的垂直平分线与x轴的交点为圆心，根据直角三角形有

解得

，则粒子做圆周运动的的圆心角为120°，周期为

粒子做圆周运动的向心力由洛仑兹力提供，根据牛顿第二定律得

，，化简得

（2）仍在磁场中的粒子其圆心角一定大于120°，这样粒子角度最小时从磁场右边界穿出；角度最大时从磁场左边界穿出。

角度最小时从磁场右边界穿出圆心角120°，所经过圆弧的弦与⑴中相等穿出点如图，根据弦与半径、x轴的夹角都是30°，所以此时速度与y轴的正方向的夹角是60°。

角度最大时从磁场左边界穿出，半径与y轴的的夹角是60°，则此时速度与y轴的正方向的夹角是120°。

所以速度与y轴的正方向的夹角范围是60°到120°

（3）在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切，在三角形中两个相等的腰为，而它的高是

，半径与y轴的的夹角是30°，这种粒子的圆心角是240°。所用时间为。

所以从粒子发射到全部离开所用时间为。

知识点

带电粒子在匀强磁场中的运动

1

题型：简答题

|

简答题 · 8 分

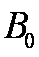
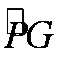
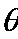
右图中左边有一对平行金属板，两板相距为d，电压为V；两板之间有匀强磁场，磁感应强度大小为，方向与金属板面平行并垂直于纸面朝里。图中右边有一半径为R、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为B，方向垂直于纸面朝里。一电荷量为q的正离子沿平行于全属板面、垂直于磁场的方向射入平行金属板之间，沿同一方向射出平行金属板之间的区域，并沿直径EF方向射入磁场区域，最后从圆形区城边界上的G点射出，已知弧所对应的圆心角为，不计重力，求

（1）离子速度的大小；

（2）离子的质量。

正确答案

见解析

解析

由题设知，离子在平行金属板之间做匀速直线运动，安所受到的向上的压力和向下的电场力平衡

①

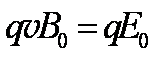
式中，是离子运动速度的大小，是平行金属板之间的匀强电场的强度，有

②

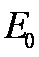
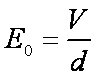
由①②式得 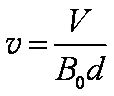③

（2）在圆形磁场区域，离子做匀速圆周运动，由洛伦兹力公式和牛顿第二定律有

④

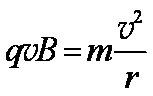
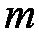
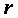
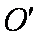
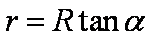
式中，和分别是离子的质量和它做圆周运动的半径。由题设，离子从磁场边界上的点G穿出，离子运动的圆周的圆心必在过E点垂直于EF的直线上，且在EG的垂直一平分线上(见右图)。由几何关系有

⑤

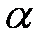
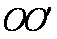
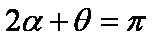
式中，是与直径EF的夹角，由几何关系得

⑥

联立③④⑤⑥式得，离子的质量为 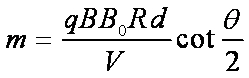⑦

知识点

带电粒子在匀强磁场中的运动带电粒子在混合场中的运动

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点