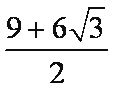- 向量在几何中的应用
- 共173题
已知椭圆






(1)求椭圆
(2)过椭圆左焦点





正确答案
见解析。
解析
(1)



∴椭圆E的方程为:
(2)设点

由方程组


由已知得:
知识点
已知等边


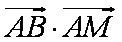
正确答案
解析
略
知识点
如图,设椭圆中心在坐标原点,




(1)若

(2)求四边形
正确答案
见解析
解析
(1)依题可设得椭圆的方程为
直线
设



由
点

所以

(2)解法1:根据点到直线的距离公式和①式知,点

又

当



解法2:由题设,
设






知识点
如图,圆周角







(1)求证:
(2)若





正确答案
见解析
解析
(1)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
所以∠EDC=∠DCB,
所以BC∥DE,
(2)解:因为D,E,C,F四点共圆,所以∠CFA=∠CED
由(1)知∠ACF=∠CED,所以∠
设∠DAC=∠DAB=x,
因为
所以∠CFA=∠FBA+∠FAB=3x,
在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,

知识点
已知椭圆







(1)求椭圆
(2)求
(3)若



正确答案
见解析。
解析
(1)易知



故方程为
(2)证明:设





设

∴
=


故所求范围是
(3)由对称性可知N

直线AN:


∴直线

知识点
扫码查看完整答案与解析