- 曲线与方程
- 共922题
曲线

正确答案
(3,

解析
解:联立两函数的解析式,可得:
解得
即曲线



故答案为:(3,

已知曲线C的方程为:x2+y2-2|x|-2|y|=0,P1、P2是曲线C上的两个点,则|P1P2|的最大值为______.
正确答案
解析
解:利用绝对值的几何意义可知曲线C表示x2+y2-2x-2y=0,x2+y2+2x|-2y=0,x2+y2+2x+2y=0,x2+y2-2x+2y=0,分别在各个象限的部分(包括与坐标轴的交点)
∵P1、P2是曲线C上的两个点,
∴|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长
∴|P1P2|的最大值为2



故答案为:
平面上动点A(x,y)满足

正确答案
解析



∵B(-4,0),C(4,0),
∴|AB|+|AC|≤10,当且仅当A为(0,±3)时,等号成立.
故选:B.


(1)求曲线ABCD的方程;
(2)曲线ABCD和x轴围成的图形面积.
正确答案
解:(1)设圆心为E(0,a),则EC=ED,所以(
过AB的直线为y=k(x+3)(k>0),则
∴ABCD的方程,一段为AB:x-y+3=0(-3,-1),一段为BCD:x2+(y-1)2=2(
(2)连接BE,则BD为圆E的直径
∴曲线ABCD和x轴围成的图形面积等于Rt△ABD的面积加上半圆的面积
即
解析
解:(1)设圆心为E(0,a),则EC=ED,所以(
过AB的直线为y=k(x+3)(k>0),则
∴ABCD的方程,一段为AB:x-y+3=0(-3,-1),一段为BCD:x2+(y-1)2=2(
(2)连接BE,则BD为圆E的直径
∴曲线ABCD和x轴围成的图形面积等于Rt△ABD的面积加上半圆的面积
即
设a,b∈R,ab≠0,则直线ax-y+b=0和曲线bx2+ay2=ab的大致图形是( )
正确答案
解析
解:整理曲线的方程得
对于A选项观察直线图象可知斜率小于0即,a<0,b>0
则曲线的方程的图象一定是双曲线,故A不符合.
B,D选项中,直线的斜率a>0,截距b<0,则曲线方程为双曲线,焦点在x轴,故B正确,D错误.
C项中直线斜率a<0,则曲线一定不是椭圆,故C项错误.
故选B
命题A:两曲线F(x,y)=0和G(x,y)=0相交于点P(x0,y0),命题B:曲线F(x,y)+λG(x,y)=0(λ为常数)过点P(x0,y0),则A是B的______条件.
正确答案
充分不必要
解析
解:∵命题A:两曲线F(x,y)=0和G(x,y)=0相交于点P(x0,y0),
∴F(x0,y0)=0,且G(x0,y0)=0,
∴F(x0,y0)+λG(x0,y0)=0,
∴命题B:曲线F(x,y)+λG(x,y)=0(λ为常数)过点P(x0,y0)成立,故充分性成立.
当命题B成立时,曲线F(x,y)+λG(x,y)=0(λ为常数)过点P(x0,y0),
∴F(x0,y0)+λG(x0,y0)=0,
但不能推出F(x0,y0)=0,且 G(x0,y0)=0,只能得出F(x0,y0)=-λG(x0,y0),
故必要性不成立,
故答案为:充分不必要条件.
设A、B分别是直线y=




正确答案
解:设P(x,y),因为A,B分别是直线y=

故可设
又

因为
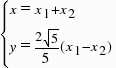

代入①得:

解析
解:设P(x,y),因为A,B分别是直线y=

故可设
又

因为
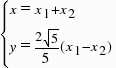

代入①得:

方程
正确答案
解析
解:由
得
即
也就是动点(x,y)到定点(-3,1)的距离与到定直线x-y+3=0的距离的比等于
符合双曲线的定义,
∴该方程表示的曲线是双曲线.
故选:C.
已知曲线C:

正确答案
解:设直线l的方程为y=tx+1,P(x,y),则k=


y=tx+1代入曲线C:

∵AB的中点为P,
∴x=
∴k=t+

解析
解:设直线l的方程为y=tx+1,P(x,y),则k=


y=tx+1代入曲线C:

∵AB的中点为P,
∴x=
∴k=t+

已知实数x,y满足方程x2+y2+4y-96=0,有下列结论:
①x+y的最小值为
②对任意实数m,方程(m-2)x-(2m+1)y+16m+8=0(m∈R)与题中方程必有两组不同的实数解;
③过点M(0,18)向题中方程所表示曲线作切线,切点分别为A,B,则直线AB的方程为y=3;
④若x,y∈N*,则xy的值为36或32.
以上结论正确的有______(用序号表示)
正确答案
①③④
解析
解:方程x2+y2+4y-96=0 即 x2+(y+2)2=100,表示以(0,-2)为圆心,以10为半径的圆.
令x=10cosθ,y=-2+10sinθ,有x+y=-2+10

方程(m-2)x-(2m+1)y+16m+8=0(m∈R) 即 m(x-2y+16)-(2x+y-8)=0,
表示过x-2y+16=0 与2x+y-8=0交点(0,8)的直线系,而点(0,8)在圆上,
故有的直线和圆有两个交点,有的直线和圆有一个交点,故②不正确.
过点M(0,18)向题中方程所表示曲线作切线,切点分别为A,B,由圆的对称性、切线的对称性知,
A,B关于y轴对称.而切线MA=

点M到AB的距离为MA•cos30°=15,故AB的方程为 y=18-15=3,故③正确.
圆x2+(y+2)2=100上的坐标为正整数点有(6,6),(8,4),若x,y∈N*,则xy的值为36或32,
故④正确.
综上,①③④正确,
故答案为:①③④.
扫码查看完整答案与解析








