任意角的三角函数的定义
共29题

· 任意角的三角函数的定义

任意角的三角函数的定义
共29题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 4 分

13. 已知，且有，，则 ▲ .

正确答案

解析

已知，sinx,cosx,tanx,siny,cosy,tany>0, 将原式两边相除，得 ,分别将两式两边平方，相加消去y,得，解

考查方向

考查同角三角函数关系及其转化

解题思路

首先讲题中两个等式相除，得到x和y的余弦函数的关系，再将y的正弦值余弦值，用x的正弦值余弦值表示，用平方关系消去y得到x的三角函数等式，进而求出余弦值

易错点

不能正确的应用同角三角函数关系

知识点

任意角的三角函数的定义三角函数的化简求值

题型：填空题

填空题 · 4 分

13．已知角的顶点在坐标原点，始边与轴的正半轴重合，，角的终边与单位圆交点的横坐标是，角的终边与单位圆交点的纵坐标是（）.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的三角函数的定义同角三角函数间的基本关系两角和与差的余弦函数角的变换、收缩变换

题型：简答题

简答题 · 14 分

22．设函数f （θ）＝sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x，y），且0≤θ≤π．

（1）若点P的坐标为（），求f（θ）的值；

（2）若点P（x，y）为平面区域，上的一个动点，试确定角θ的取值范围，并求函数f（θ）的最小值和最大值．

正确答案

（1）由点P的坐标和三角函数的定义可得

sinθ＝，cosθ＝．

于是f（θ）＝sinθ＋cos θ＝＝2．

（2）作出平面区域Ω（即三角区域ABC），

其中A（1，0），B（1，1），C（0，1）．

于是0≤θ≤．

又f（θ）＝sinθ＋cosθ＝2sin（θ＋），

且≤θ＋≤，

故当θ＋＝，即θ＝时，

f（θ）取得最大值，且最大值等于2 ；

当θ＋＝，即θ＝0时，

f（θ）取得最小值，且最小值等于1．

解析

解析已在路上飞奔，马上就到！

知识点

任意角的三角函数的定义正弦函数的定义域和值域两角和与差的正弦函数

题型：简答题

简答题 · 14 分

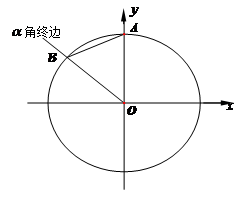
20．如图是单位圆上的动点，且分别在第一,二象限．是圆与轴正半轴的交点，为正三角形．若点的坐标为．记。

（1）若点的坐标为,求的值；

（2）求的取值范围。

正确答案

解：（1）因为A点的坐标为，根据三角函数定义可知,

，得，

所以＝

（2）因为三角形AOB为正三角形，所以，

所以==

所以=

, ,

即,

解析

解析已在路上飞奔，马上就到！

知识点

任意角的三角函数的定义同角三角函数间的基本关系二倍角的正弦二倍角的余弦两点间的距离公式

题型：简答题

简答题 · 14 分

17.如图，单位圆（半径为的圆）的圆心为坐标原点，单位圆与轴的正半轴交于点，与

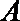
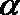
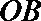
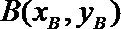
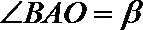
钝角的终边交于点，设。

（1）用表示；

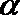
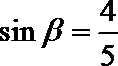
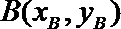
（2）如果，求点的坐标；

（3）求的最小值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的三角函数的定义利用基本不等式求最值圆方程的综合应用

题型：单选题

单选题 · 5 分

7．若点在直线上，则的值等于

正确答案

解析

由点在直线上知，故

，故选择B选项。

考查方向

本题主要考查了任意角三角函数的定义及诱导公式及倍角公式,为高考常考题，在近几年的各省高考题出现的频率较高，常与三角函数的定义、诱导公式、倍角公式等知识点交汇命题。

解题思路

先根据点在直线上求出，再利用诱导公式及倍角公式即可求出的值。

易错点

求时因诱导公式不熟悉导致出错。

知识点

任意角的三角函数的定义同角三角函数间的基本关系诱导公式的作用二倍角的余弦

题型：单选题

单选题 · 5 分

16．已知点的坐标为，将绕坐标原点逆时针旋转至，则点的纵坐标为（）

正确答案

解析

，即点的纵坐标为

知识点

任意角的三角函数的定义

题型：单选题

单选题 · 5 分

7．若点在直线上，则的值等于

正确答案

解析

因为点在直线上，所以，从而，，所以选B选项。

考查方向

本题主要考查了同角三角函数的基本关系式，诱导公式以及三角恒等变换问题，考查了转化化归思想方法。

解题思路

首先由点P在直线上，可以求得，再利用诱导公式以及三角恒等变换可以求得最终结果。

易错点

1、本题易在使用诱导公式时判断错误符号而导致出错。

2、本题容易因为公式记忆不清楚而出现错误。

知识点

任意角的三角函数的定义同角三角函数间的基本关系诱导公式的作用二倍角的余弦

题型：单选题

单选题 · 5 分

5．设 a=sin46°，b=cos46°，c=tan46°．则（　　）

Ac＞a＞b

Ba＞b＞c

Cb＞c＞a

Dc＞b＞a

正确答案

考查方向

本题主要考查了任意角的三角函数的定义，三角函数线的应用研究，在近几年的各省高考题出现的频率较高，常以三角公式与三角函数等知识交汇命题，较难。

易错点

1、本题在把题意转化成利用三角函数线去研究上易出错。(方法二)

知识点

任意角的三角函数的定义三角函数线

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 三角函数线

百度题库 > 高考 > 理科数学 > 任意角的三角函数的定义

扫码查看完整答案与解析