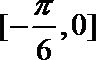- 正弦函数的单调性
- 共92题
设△ABC的三个内角A、B、C所对的三边分别为a, b, c,若△ABC的面积为S = a2-(b-c)2,则
正确答案
4
解析
易知:




知识点
在
(1)角A,B,C成等差数列,求
(2)若

正确答案
(1)
解析
知识点
已知


(1)求方程
(2)求函数
正确答案
见解析
解析
(1)
由


故方程

(2)

∴函数

由
故函数

知识点
在



(1)求函数
(2)若函数


正确答案
见解析
解析
(1)依题意得


所以

(2)由(1)知:由



知识点
函数
(1)求函数
(2)求函数


正确答案
见解析
解析
解(1)由图知
∴


∵


∴

∵


(2)由
解得函数

函数

知识点
已知函数
(1)当

(2)设△ABC的内角A,B,C的对应边分别为a,b,c,且


正确答案
见解析
解析
(1)

令
解得



(2)由
而


因为向量


由正弦定理得:
由余弦定理得:
由①②解得
知识点
4.函数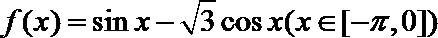
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆







(1)求直线


(2)设直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析