- 正弦函数的单调性
- 共92题
1
题型:
单选题
|
16. 若


正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的单调性
1
题型:简答题
|
20.已知向量


(1)求函数
(2)当

(3)说明

正确答案
(2)由
解得
∵取k=0和1且


∴


法二:∵

∴由

解得

∴


(3)



再把所得各点的横坐标缩短到原来的
最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),
得到
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的单调性函数y=Asin(ωx+φ)的图象变换三角函数中的恒等变换应用平面向量数量积的运算
1
题型:简答题
|
16.已知函数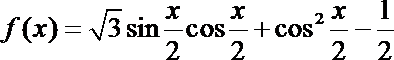
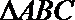
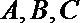
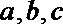
(I)求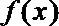
(Ⅱ)若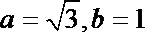
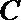
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用正弦定理
1
题型:简答题
|
22.如图,椭圆

(1)求椭圆C的标准方程;
(2)已知顶点在坐标原点的抛物线的焦点为椭圆的上焦点



(3)若直线


正确答案
答案:
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的单调性
1
题型:填空题
|
15.三棱锥A-BCD中,BA


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的单调性
下一知识点 : 正弦函数的对称性
扫码查看完整答案与解析