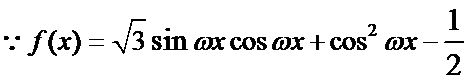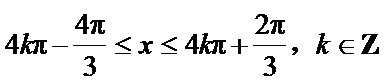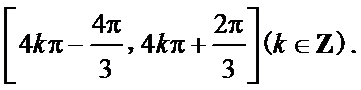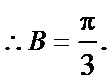正弦函数的单调性
共92题

· 正弦函数的单调性

正弦函数的单调性
共92题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

11．函数的单调增区间为（）

正确答案

（也可以写成）

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

5.函数y=3cos(2x+)(-≤x≤)与y=3cos(2x-π)(π≤x≤π)的图象和两直线y=±3所围成的封闭区域的面积为（）

A8π

B6π

C4π

D以上都不对

正确答案

解析

∵函数y=3cos(2x-π)=3cos[2(x-π)+]，

∴y=3cos(2x-π)的图象是将函数y=3cos(2x+)的图象向右平移π个单位得到的.

由画图（图略）可知，所围成的区域的面积为π×6=8π.

知识点

正弦函数的单调性

题型：单选题

单选题 · 5 分

6.已知函数f(x)=sin ωx (ω>0)在区间上是单调减函数，则ω满足的条件是（）

A(0，3]

B[3，]

C(0，]

D[3，+∞)

正确答案

解析

函数f(x)=sin ωx的图象如图

由题意知得3≤ω≤，故选B.

知识点

正弦函数的单调性

题型：单选题

单选题 · 5 分

10．已知函数，则下列结论正确的是( )

A函数在区间上为增函数

B函数的最小正周期为

C函数的图像关于直线对称

D将函数的图像向右平移个单位，再向上平移1个单位，得到函数的图像。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

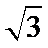
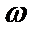
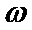
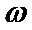
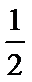
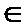
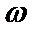
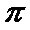
17．已知函数f(x)=（sinx+ cosx）cosx一（xR，>0）．若f(x)）的最小止周期为4．

（I）求函数f(x)的单调递增区间；

（II）在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a-c)cosB=bcosC，求函数f（A）的取值范围．

正确答案

（1）的单调递增区间为；

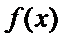
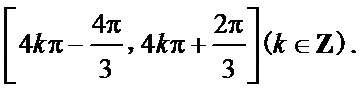
（2）．

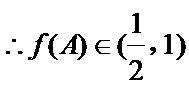
解析

试题分析：本题属于三角函数、解三角形中的基本问题，题目的难度是逐渐由易到难，具体解析如下：

（I）

．

，．由，

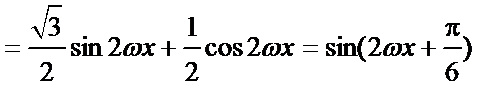
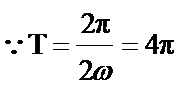
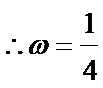
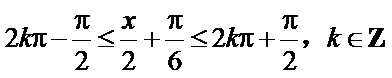
得

∴的单调递增区间为

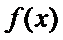
（Ⅱ）由正弦定理得，， ∴．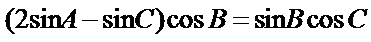

或：，，∴．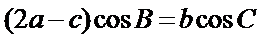

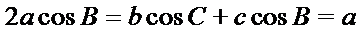
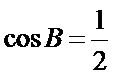
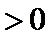
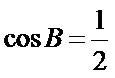
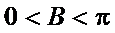
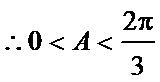
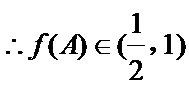
∵，∴．又，

．．．

考查方向

本题考查了三角函数的化简与求值，大体可以分成以下几类：

1、由y=Asin（ωx+φ）的部分性质确定其解析式；

2、三角函数的恒等变换及化简求值；

3、正余弦定理的综合运用；

4、三角形中的几何计算；

5、三角函数的最值等．

解题思路

本题考查三角函数以及解三角形，解题步骤如下：

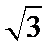
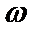
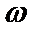
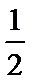
1、化简f(x)=（sinx+ cosx）cosx一；

2、求函数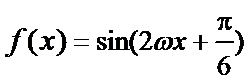的单调递增区间；

3、根据三角形内角和，利用三角恒等变换求出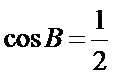，进而求出角B的值；

4、利用三角形内角和得出角A的范围，求出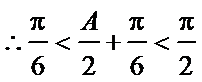，进而求出答案。

易错点

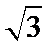
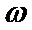
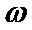
1、化简f(x)=（sinx+ cosx）cosx一的时候出错；

2、求单调区间时候范围不清导致出错；

3、在化简求值时，角的范围不清导致出错。

知识点

三角函数的周期性及其求法正弦函数的单调性三角函数中的恒等变换应用正弦定理三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 正弦函数的对称性

百度题库 > 高考 > 文科数学 > 正弦函数的单调性

扫码查看完整答案与解析