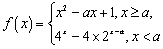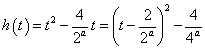- 函数的概念及其构成要素
- 共1288题
定义:对于函数








(1)证明函数

(2)试判断函数




(3)设函数






正确答案
见解析
解析
(1)

所以函数
(2)函数


是广义周期函数, 且
(非零常数)。 -------------------------------------------------------------------------------------( 8分)
(3)
所以

设

由

又








由


又







知识点
已知函数
(1) 若


(2) 若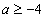



正确答案
见解析。
解析
(1) 因为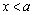
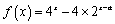
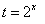
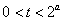
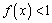
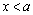
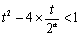
即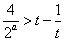
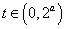
令p (t)=t-,
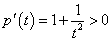
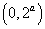
所以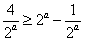
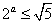
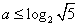
(2) 当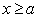
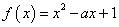
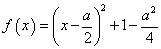
当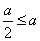
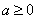
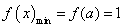
当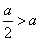
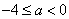
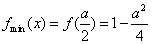
当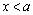
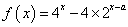
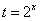
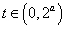
当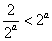
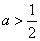
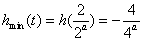
当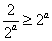
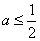
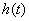
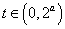
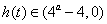
无最小值;
综合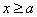
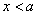
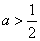
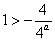
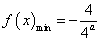
当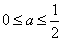
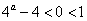
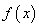
当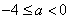
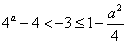
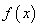
综上所述,当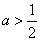
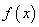
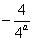
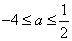
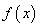
知识点
函数
正确答案
解析
略
知识点
已知函数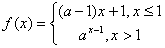
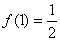
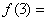
正确答案
解析
因为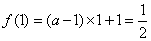
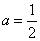
则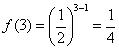
知识点
将函数

正确答案
解析



知识点
扫码查看完整答案与解析