- 函数的概念及其构成要素
- 共1288题
已知函数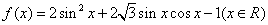
(1) 试说明函数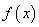
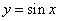
(2)若函数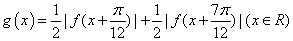
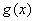
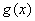
(3) 求函数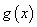
正确答案
见解析
解析
(1)∵
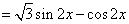
∴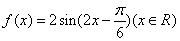
∴函数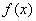
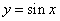
①将函数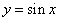
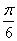
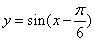
②将函数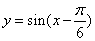
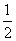
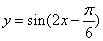
③将函数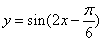
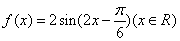
(说明:横坐标先放缩,再平移也可,即将函数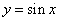
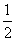

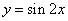
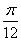
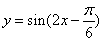
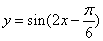
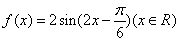
(2) 由(1)知,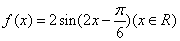
∴
又对任意
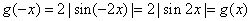
∴函数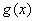
∵函数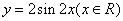
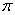
∴结合图像可知,函数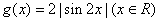

(3) 先求函数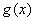
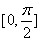
当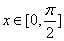
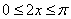
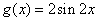
易知,此时函数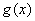
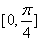
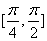
函数的取值范围是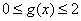
因此,依据周期函数的性质,可知函数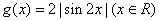
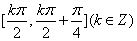
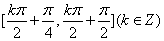
函数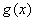
知识点
函数f(x)=
正确答案
解析
函数f(x)的定义域为[0,+∞)
∵y=

∴函数f(x)=
而f(0)=﹣1<0,f(1)=
故函数f(x)=
故选B
知识点
已知函数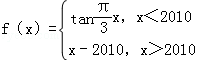
正确答案
0
解析
∵函数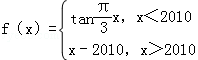
∴f(2013)=2013﹣2010=3
则f[f(2013)]=f(3)=tanπ=0
故答案为:0
知识点
已知曲线C的参数方程为
正确答案
3
解析
∵曲线C的参数方程为
平方相加可得 (x﹣2)2+y2=1,表示以(2,0)为圆心,以1为半径的圆。
圆心到直线的距离等于
故曲线上C的点到直线3x﹣4y+4=0的距离的最大值为2+r=2+1=3。
知识点
设函数
(1)当


(2)设


(3)设



正确答案
见解析
解析
解析:(1)


所以
(2)证明:因为 









(3)当n=2时,f2(x)=x2+bx+c.
对任意x1,x2∈[-1,1]都有|f2(x1)-f2(x2)|≤4等价于f2(x)在[-1,1]上的
据此分类讨论如下:
①当
②当-1≤


③当0≤


综上可知,-2≤b≤2.
注:②,③也可合并证明如下:
用max{a,b}表示a,b中的较大者。
当


=
=1+c+|b|-(
=(1+
知识点
扫码查看完整答案与解析