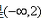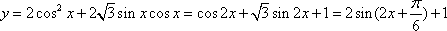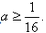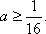- 函数的概念及其构成要素
- 共1288题
已知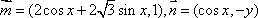
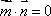
(1)将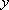

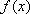
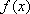
(2)当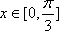
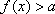

正确答案
(1)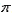
解析
解析:(1)由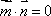
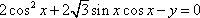
即
所以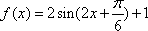
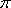
(2)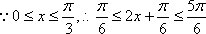
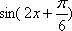

由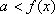
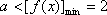
所以实数
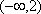
知识点
已知二次函数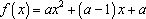
(1)函数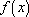
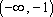

(2)关于
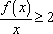
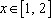

(3)函数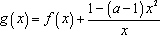
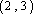

正确答案
(1)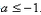
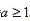
解析
解析:(1)当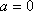
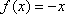
当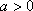
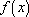
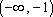

当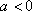
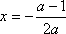
由条件得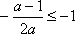
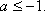
(2)设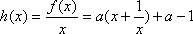
当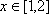
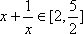
因为不等式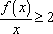
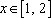
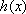
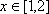
所以,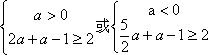
解得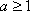
(3)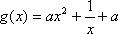
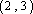
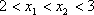
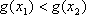
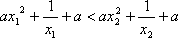
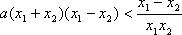
因为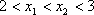
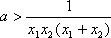
而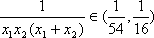
所以
知识点
已知函数
(1)求函数
(2)若对任意



正确答案
见解析
解析
(1)解:因为

当


当


故
当


故

综上所述,当

当


当

(2)解:,由(1)知,




所以函数


函数


由于对任意


所以
解得
因为对任意

所以实数
知识点
设函数






(1)判断函数


(2)设函数



(3)若


正确答案
见解析
解析
(1)因为

同理

(2)因为

函数

又因为
……………9分
所以
(3)因为


即
所以
由

若


若



若



知识点
已知函数
(1)求


正确答案
见解析
解析
(1)解:

(2)解法1:因为

所以

因为
由①、②解得
所以

解法2:因为

所以

知识点
扫码查看完整答案与解析