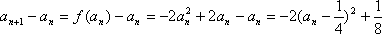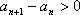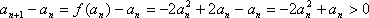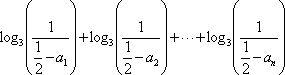- 函数的概念及其构成要素
- 共1288题
已知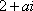
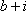
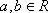
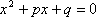
(1)求
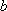
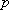
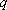
(2)计算: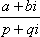
正确答案
见解析
解析
(1)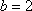
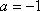
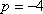
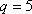
(2)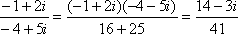
知识点
已知函数
(1)画出函数

(2)解关于

(3)当


正确答案
见解析
解析
(1)坐标系正确1分;
大致图像3分.评分关键点:与




(2)原不等式等价转化为下列不等式组:






(或者由


所以原不等式的解为:

(3)证法1:原不等式等价转化为下列不等式组:
(Ⅰ)

(Ⅰ)不等式2中,判别式






(Ⅱ)在不等式4中,判别式



又
所以,
(或者
所以当

综上讨论,得到:当


证法2:设





以下讨论关于
知识点
已知函数

(1)求函数
(2)当


(3)若



正确答案
见解析。
解析
(1)


(2) 

又f(x)在 (m,2m+1)上为增函数
(3)直线l在P点的切线斜率
令
当
知识点
设
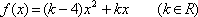

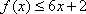
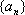
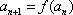
(1)求函数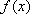
(2)试写出一个区间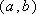
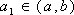
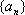
(3)已知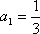
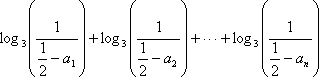
正确答案
见解析
解析
(1)由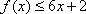
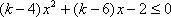
从而得: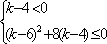
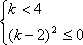
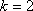
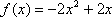
其值域为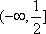
(2)当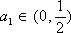
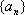

设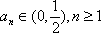
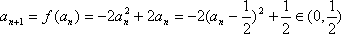
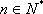
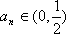
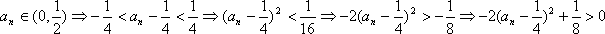
从而得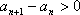
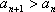
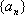
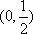
注
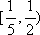
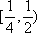
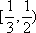

另解:若数列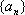
即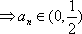

又当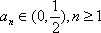
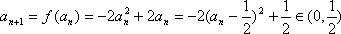
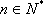
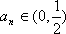
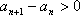
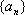
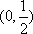
(3)由(2)知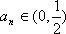
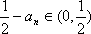
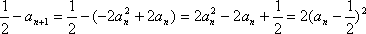
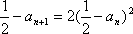
令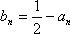
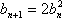
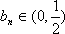
从而有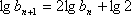
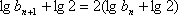
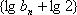
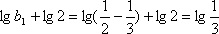
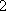
从而得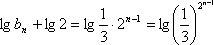
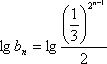
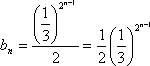
所以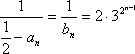
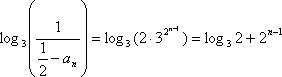
所以,
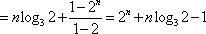
知识点
已知向量


(1)求函数
(2)记△





正确答案
见解析
解析
(1)

所以
递减区间是
(2)由


当




当




知识点
扫码查看完整答案与解析