直线与平面平行的判定与性质
共228题

· 直线与平面平行的判定与性质

直线与平面平行的判定与性质
共228题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

如图，四棱锥中，,分别为线段的中点。

（1）求证：

（2）求证：

正确答案

;见解析。

解析

（1）连接AC交BE于点O，连接OF，不妨设AB=BC=1,则AD=2

四边形ABCE为菱形

又

（2）

知识点

直线与平面平行的判定与性质直线与直线垂直的判定与性质

题型：简答题

简答题 · 12 分

如图，四棱锥中，,,分别为的中点

（1）求证：

（2）求证：

正确答案

见解析。

解析

知识点

直线与平面平行的判定与性质平面与平面垂直的判定与性质

题型：简答题

简答题 · 14 分

（如图，在四面体中，点分别是棱的中点。

(1) 求证：平面；

(2) 求证：四边形为矩形；

(3 是否存在点，到四面体六条棱的中点的距离相等？说明理由。

正确答案

略

解析

（1）因为D，E分别为AP，AC的中点，

所以DE//PC。

又因为DE平面BCP，

所以DE//平面BCP。

（2）

因为D，E，F，G分别为AP，AC，BC，PB的中点，

所以DE//PC//FG，DG//AB//EF。

所以四边形DEFG为平行四边形，

又因为PC⊥AB，所以DE⊥DG，

所以四边形DEFG为矩形。

（3）存在点Q满足条件，理由如下：连接DF，EG，设Q为EG的中点，

由（2）知，DF∩EG=Q，且QD=QE=QF=QG=EG。

分别取PC，AB的中点M，N，连接ME，EN，NG，MG，MN。

与（2）同理，可证四边形MENG为矩形，其对角线点为EG的中点Q，

且QM=QN=EG，所以Q为满足条件的点。

知识点

直线与平面平行的判定与性质

题型：单选题

单选题 · 5 分

设集合A={}，集合B为函数的定义域，则AB=

A（1，2）

B[1，2]

C[ 1，2）

D（1，2 ]

正确答案

解析

，

知识点

直线与平面平行的判定与性质

题型：简答题

简答题 · 12 分

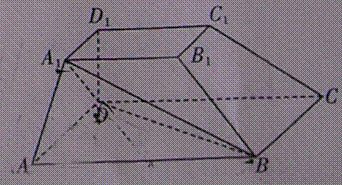
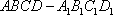
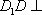
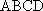
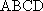
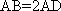
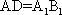
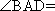
如图，在四棱台中，平面，底面是平行四边形，，，60°

（1）证明：；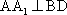

（2）证明：.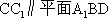

正确答案

见解析。

解析

（1）证明：因为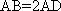，所以设

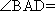
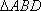
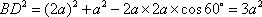
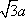
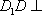
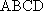
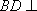
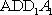
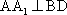
AD=a,则AB=2a,又因为60°,所以在中,由余弦定理得：,所以BD=,所以,故BD⊥AD,又因为

平面，所以BD,又因为, 所以平面,故.

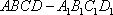
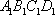
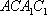
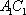
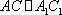
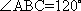
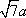
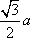
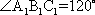
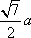
(2)连结AC,设ACBD=0, 连结,由底面是平行四边形得:O是AC的中点,由四棱台知:平面ABCD∥平面,因为这两个平面同时都和平面相交,交线分别为AC、，故，又因为AB=2a, BC=a, ，所以可由余弦定理计算得AC=，又因为A1B1=2a, B1C1=, ，所以可由余弦定理计算得A1C1=，所以A1C1∥OC且A1C1=OC，故四边形OCC1A1是平行四边形，所以CC1∥A1O，又CC1平面A1BD，A1O平面A1BD，所以.

知识点

异面直线及其所成的角空间中直线与直线之间的位置关系直线与平面平行的判定与性质直线与直线垂直的判定与性质

继续学习学习下一知识点

下一知识点 : 平面与平面平行的判定与性质

百度题库 > 高考 > 文科数学 > 直线与平面平行的判定与性质

扫码查看完整答案与解析