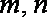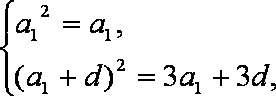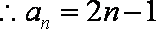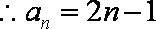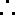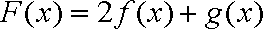- 直线与平面平行的判定与性质
- 共228题
如图,在直三棱柱



(1)求三棱柱

(2)求异面直线

正确答案
见解析
解析
(1)在△





所以

(2)连结





在△



由余弦定理,

即异面直线


知识点
已知数列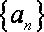
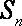
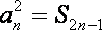
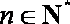
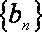
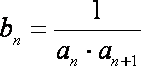
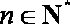
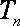
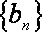
(1)求数列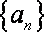

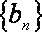
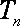
(2)若对任意的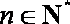
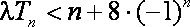
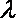
(3)是否存在正整数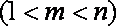
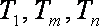

正确答案
(1)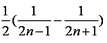
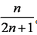
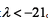
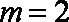


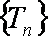
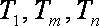

解析
解析:(1)(法一)在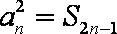
得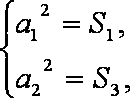
解得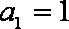
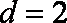
又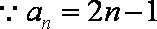
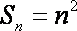
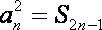
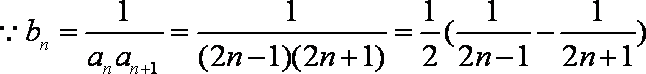

(2)①当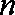
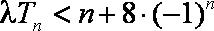

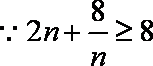
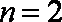
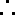

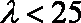
②当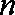
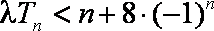
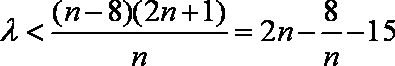
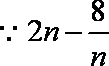
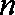
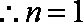
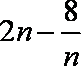
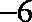

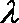
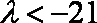
综合①、②可得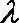
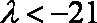
(3)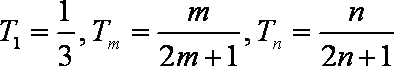
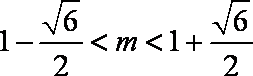
若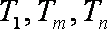
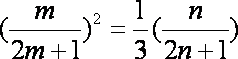
即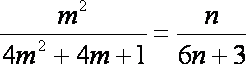
由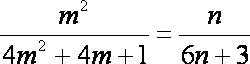
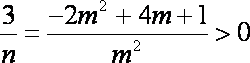
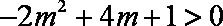
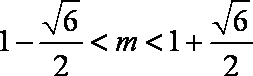
又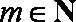
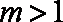
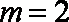

因此,当且仅当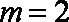


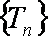
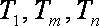

[另解] 因为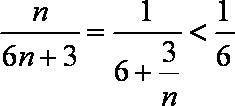
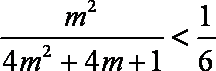
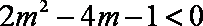
知识点
已知
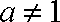
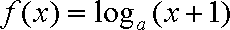
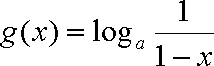
(1)求函数

(2)若关于
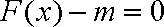
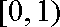
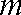
正确答案
(1)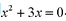
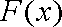



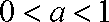

解析
解析:(1)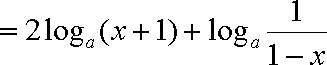

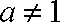
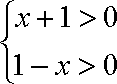

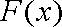
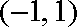
令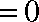
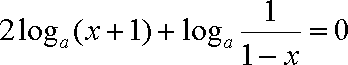
方程变为
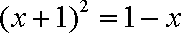
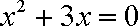
解得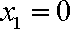
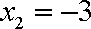
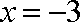
即函数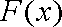

(2)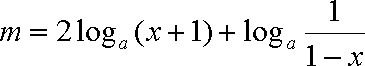
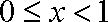
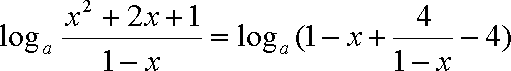
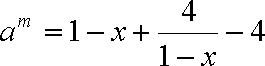
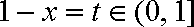
函数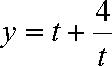
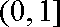
当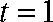

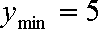
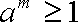
①若

②若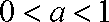

知识点
如图,在棱长为





(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)






(2)取


由于




在


由余弦定理得,
所以
即异面直线


知识点
如图,在直三棱柱






(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)
(2)连接




在


所以异面直线


知识点
扫码查看完整答案与解析