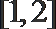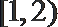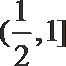- 导数及其应用
- 共3028题
若函数


正确答案
解析
由图知,

∴


解得
知识点
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中M、P及图中a的值;
(2)若该校高一学生有360人,试估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)学校决定对参加社区服务的学生进行表彰,对参加活动次数在[25,30)区间的学生发放价值80元的学习用品,对参加活动次数在


正确答案
见解析。
解析
(1)由题可知 


又
解得 


则

(2)由(1)知,参加服务次数在区间

(3)所取出两人所获得学习用品价值之差的绝对值可能为0元、20元、40元、60元,则




所以


知识点
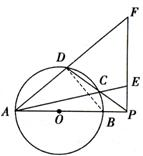
如图,圆
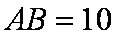
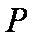
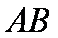
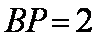
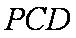


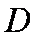
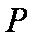
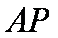
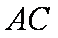
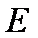

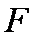
(1)求证: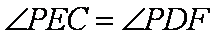
(2)求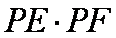
正确答案
见解析
解析
解法1:(1)连接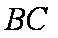
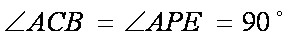
即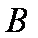
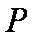
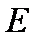

∴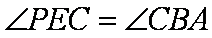
又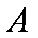
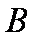

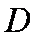
∴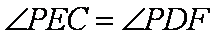
∵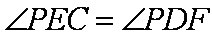
∴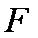
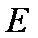

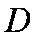
∴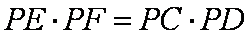
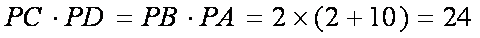
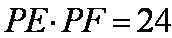
解法2:(1)连接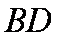
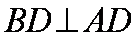
∴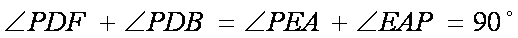
∵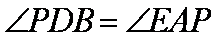
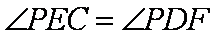
(2)∵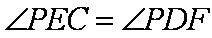
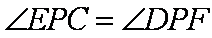
∴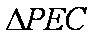
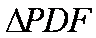
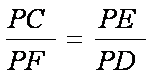
即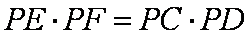
又∵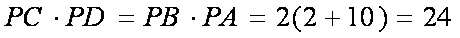
∴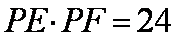
知识点
22.如图,四边形







(1)求
(2)若



正确答案
见解析。
解析
(1)由



设

所以
(2)
知识点




正确答案
3或
解析
由二项式定理可知



知识点
如图,焦距为2的椭圆E的两个顶点分别为



(1)求椭圆E的标准方程;
(2)若直线
正确答案
(1)
解析
(1)设椭圆E的标准方程为






∴

(2)设


消去y,得,
∴


∵原点O总在以PQ为直径的圆内,∴

又
由


故实数m的取值范围是
知识点
如图所示,程序框图(算法流程图)的输出结果是( )
正确答案
解析
程序在运行过程中各变量的值如下表示:
s i 是否继续循环
循环前 1 1/
第一圈 1 2 是
第二圈 2 3 是
第三圈 6 4 是
第四圈 24 5 否
故最后输出的i值为:5,
知识点
某家具厂生产一种儿童用组合床柜的固定成本为20000元,每生产一组该组合床柜需要增加投入100元,已知总收益满足函数:

(1)将利润

(2)当月产量为何值时,该厂所获得利润最大?最大利润是多少?(总收益=总成本+利润)
正确答案
见解析。
解析
(1)由题设,总成本为
则
(2)当

当

当

则
∴当

知识点
19.为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示。
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图)再根据频率分布直方图估计这500名志愿者中年龄在 [30,35)岁的人数;
(2)在抽出的100名志原者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学 期望
正确答案
见解析。
解析
(1)0.2×100=20,
∴①处是20,②处是0.35,
∵由频率分步直方图中,[30,35)的人数是0.35×500=175
在频率分步直方图知,在[25,30)这段数据上对应的频率是0.2,
∵组距是5,
∴小正方形的高是
在频率分步直方图中补出高是0.04的一个小正方形。
(2)用分层抽样方法抽20人,
则年龄低于30岁的有5人,年龄不低于30岁的有15人,
故X的可能取值是0,1,2,
P(X=0)=

∴X的分布列是
∴X的期望值是EX=
知识点
10.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b),满足f′(x1)=


正确答案
解析
略。
知识点
14. 若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知
(1) 当a=1时求不等式
(2) 如果函数y=
正确答案
见解析。
解析
(1)f(x)=|2x-1|+x-5=
∴f(x)=|2x-1|+x-5≥0:化为

解得:{x|x≥2或x≤-4}.
(Ⅱ)
由f(x)=0得,|2x-1|=-ax+5.
令y=|2x-1|,y=-ax+5,作出它们的图象,可以知道,当-2<a<2时,这两个函数的图象有两个不同的交点,所以,函数y=f(x)有两个不同的零点.
知识点
1.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.函数

(1)求实数a的值;
(2)若对

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析