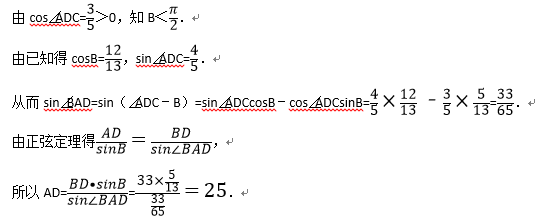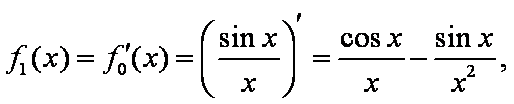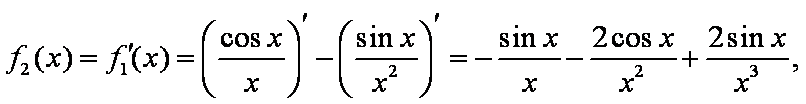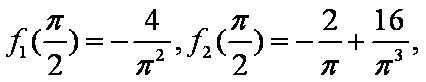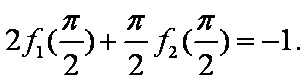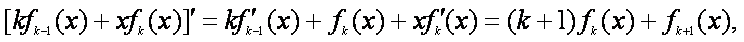- 导数及其应用
- 共3028题
给出下列函数:①




正确答案
解析
略
知识点
设



正确答案
4028
解析

令

则

知识点
若
正确答案
1
解析
知识点
定义在区间










正确答案
①④
解析
略
知识点
△ABC中,D为边BC
上的一点,BD=33,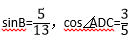
正确答案
见解析。
解析
知识点
已知函数


(1)讨论
(2) 若不等式

(3)若方程


正确答案
见解析。
解析
(1)

其导数
①当


②当



所以,

(2)当



能使

当

问题化为求

由于







即

(3)由于



构造函数:

所以函数



于是





知识点
定义在R上的函数



①若


②若函数





③函数

④若

正确答案
解析
略
知识点
曲线

正确答案
解析
略
知识点
已知函数

正确答案
解析
略
知识点
已知函数f(x)=lnx-a2x2+ax.
(1)若a=1,求函数f(x)的最大值;
(2)若函数f(x)在区间(1,+∞)上是减函数,求实数a的取值范围.
正确答案
见解析
解析
(1)当


………………………… 1分
所以



因为

所以当



所以函数


………………………… 4分
所以当

即

(2)因为

所以
①当

所以

②当



所以


所以

③当



所以


所以

综上所述,实数
………………………… 13分
知识点
已知矩阵





正确答案
见解析。
解析




知识点
某工厂生产某种产品,每日的成本C(单位:万元)与日产量x(单
位:吨)满足函数关系式C=3+x,每日的销售额S(单位:万元)与日产量x的函数关
系式
(1)求k的值;
(2)当日产量为多少吨时,每日的利润达到最大,并求出最大值。
正确答案
(1)18(2)5吨;6万元
解析
解析:(1)依题意得当x=2时L=3
(2)①当0<x<6时
②当x≥6时,显然有L≤5(当且仅当x=6时取“=”号)
综上知:当日产量为5吨时,每日的利润达到最大,最大值为6万元。
知识点
某工厂生产某种产品,已知该产品的月生产量

正确答案
见解析。
解析
每月生产x吨时的利润为
由
得当 
∴
故
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
知识点
已知函数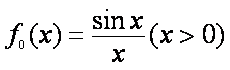
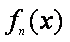
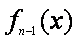
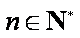
(1)求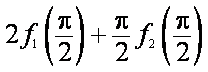
(2)证明:对任意的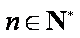
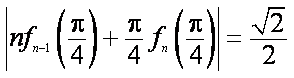
正确答案
见解析。
解析
(1)由已知,得
于是
所以
故
(2)证明:由已知,得
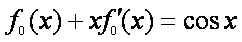
即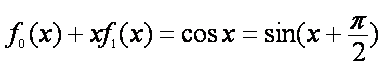
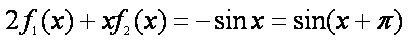
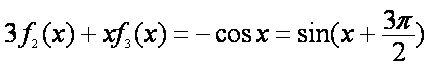
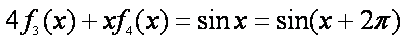
下面用数学归纳法证明等式
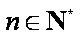
(i)当n=1时,由上可知等式成立.
(ii)假设当n=k时等式成立, 即
因为
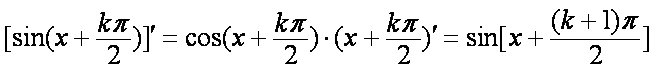
所以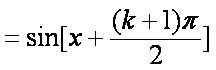
所以当n=k+1时,等式也成立.
综合(i),(ii)可知等式
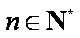
令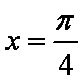
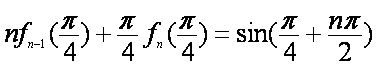
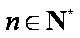
所以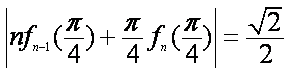
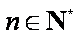
知识点
在平面直角坐标系


线段AB的垂直平分线与双曲线相交于C、D两点。
(1)求直线AB与CD的方程;
(2)判断A、B、C、D四点是否共圆?若共圆,请求出圆的方程;若不共圆,请说明理由。
正确答案
见解析
解析
(1)设A


解得




所以



(2)A、B、C、D四点共圆,下证之:
证明:由



由三点A、B、C可先确定一个圆
经检验
知识点
扫码查看完整答案与解析