- 导数及其应用
- 共3028题
已知





(1)求
(2)求函数
正确答案
(1)
解析
(1)设


则由

可得

(2)


所以,当


知识点
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,f(x) 表示C到A距离4倍与C到B距离的6倍的和.
(1)求f(x)的解析式及其定义域;
(2)要使f(x)的值不超过70,x 应该在什么范围内取值?
正确答案
见解析
解析
解析:(1)
(2)依题意,x满足 {
解不等式组,其解集为[9,23]所以 
知识点
已知





则
正确答案
2
解析
解析:提示:∵


∴根据数量积意义
同理
∵


∴

∴
知识点
已知


(1)求实数
(2)求矩阵
正确答案
见解析
解析
(1)由



(2)由(Ⅰ) 知

知识点
3.下列函数中,其图象既是轴对称图形又在区间(0,+∞)上单调递增的是( )
正确答案
解析
对于A,函数y=
对于B,函数y=﹣x2+1的图象是轴对称图形,在区间(0,+∞)上是单调减函数,∴不满足题意;
对于C,函数y=2x的图象不是轴对称图形,∴不满足题意;
对于D,函数y=lg|x+1|的图象是关于直线x=﹣1对称的图形,且在区间(0,+∞)上是单调增函数,满足题意.
故选:D.
知识点
若集合
正确答案
解析
集合



知识点
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PACD,PA = 1, PD=,E为PD上一点,PE = 2ED。
(1)求证:PA 
(2)求二面角D-AC-E的余弦值;
(3)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由。
正确答案
见解析
解析
(1) 


又PA 


(2)过E作EG//PA 交AD于G,从而EG 
且AG = 2GD , EG = PA =
连接BD交AC于O, 过G作GH//OD ,交AC于H,
连接EH。










(3)以AB , AD , PA为x轴、y轴、z轴建立空间直角坐标系。
则A(0 ,0, 0),B(1,0,0) ,C(1,1,0),P(0,0,1),E(0 ,



设平面AEC的法向量


则
假设侧棱PC上存在一点F, 且

(


又因为:














所以存在PC的中点F, 使得BF//平面AEC。 ----------------12分
20解析:(1)由f/(x)=


(2)当a=1时,f(x)= ln(1+x)—x. (x>-1)
f/(x)=
由f/(x)=0
当x∈(0,+∞)时,f/(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减…………………………8分
(3)由(2)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x 
∴≤
即h(x)=(ex-P)2+(P-x)2≥
知识点
如图所示的几何体中,四边形



(1)求证:

(2)求直线

正确答案
见解析
解析
(1)证明:∵四边形
∵


∴

同理

∵
∴平面

∵



(用向量法证明,同等给分)
(2)连接
∵四边形

设
∵


∵四边形

∴
∵


∴

∴

设



∴
∴
∴
设


取

又∵


∴
∴直线


知识点
3.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
正确答案
解析
略
知识点
8.根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在各项均为正数的等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.对于函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知函数
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
2.函数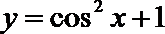
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.己知函数
(1)讨论函数
(2)设




(3)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析