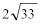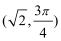导数及其应用_章节学习

1

题型：单选题

|

单选题 · 5 分

8. 对于下列命题：

①已知i是虚数单位，函数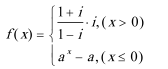在R上连续，则实数a=2.

②五本书排成一排，若A、B、C三本书左右顺序一定（不一定相邻），那么不同排法有

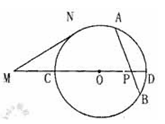
③如图，⊙O中的弦AB与直径CD相交于点p，M为DC延长线上一点，MN为⊙O的切线，N为切点，若AP＝8, PB＝6, PD＝4, MC＝6，则MN的长为

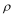
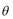
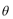
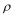
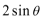
④在极坐标系（，）（0 ≤ <2π）中，曲线= 与交点的极坐标为

⑤设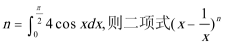的展开式的常数项为6

其中假命题的序号是（）

A②⑤

B②③

C②

D①④

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：简答题

|

简答题 · 14 分

21．已知函数，，是常数．

（1），试证明函数的图象在点处的切线经过定点；

（2）若函数图象上的点都在第一象限，试求常数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：简答题

|

简答题 · 12 分

17．设为虚数，且满足2，求。

正确答案

设，

则，

由已知得，∴=0，

∴ ，∴=1。

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 5 分

6.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧（左）视图可以为（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：填空题

|

填空题 · 5 分

13.一科研人员研究、两种菌.已知在任何时刻、两种菌的个数乘积为定值.为便于研究,科研人员用来记录菌个数的资料,其中为菌的个数,则下列说法：

①；

②若今天的值比昨天的值增加1，则今天的菌个数比昨天的菌个数多了10个；

③假设科研人员将菌的个数控制为5万个,则此时.

其中正确的序号为___________ .

正确答案

③

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 5 分

17．已知，复数，若为纯虚数，则复数的虚部为（）

A1

B

C

D0

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 5 分

6.设函数在R上的导函数为,且,下面的不等式在R内恒成立的是（）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 5 分

12．已知定义在R上的可导函数满足：，则与的大小关系是（）

A

B

C

D不确定

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

抽象函数及其应用导数的运算不等式的性质

1

题型：填空题

|

填空题 · 5 分

13．已知点M是抛物线上的动点，F为抛物线的焦点，点A在圆上，则|AM|+|MF|的最小值为___________。

正确答案

4

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：简答题

|

简答题 · 14 分

19.已知函数的图象如图，直线在原点处与函数图象相切，且此切线与函数图象所围成的区域(阴影)面积为.

（1）求的解析式

（2）若常数，求函数在区间上的最大值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算定积分

1

题型：简答题

|

简答题 · 12 分

15．已知向量，，且．

（１）求的值；

（2 ）求的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 4 分

16．已知函数的图象如下左图，则函数在上的大致图象为（　）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 5 分

11．函数f(x)的定义域是R,f(0)＝2,对任意x∈R，f(x)＋f ′(x)>1,则不等式ex·f(x)>ex＋1的解集为（）

A{x|x>0}

B{x|x<0}

C{x|x<－1，或x>1}

D{x|x<－1，或0<x<1}

正确答案

A

解析

令g（x）=ex•f（x）-ex，则g′（x）=ex•[f（x）+f′（x）-1]∵对任意x∈R，f（x）+f′（x）＞1，∴g′（x）＞0恒成立，即g（x）=ex•f（x）-ex在R上为增函数，又∵f（0）=2，∴g（0）=1故g（x）=ex•f（x）-ex＞1的解集为{x|x＞0}，即不等式ex•f（x）＞ex+1的解集为{x|x＞0}

知识点

函数单调性的性质抽象函数及其应用导数的运算

1

题型：简答题

|

简答题 · 14 分

20．已知，，，…，（）.

（Ⅰ）请写出的表达式（不需证明）；

（Ⅱ）设的极小值点为，求；

（Ⅲ）设，的最大值为，的最小值为，试求的最小值.

正确答案

（Ⅰ）（）.

（Ⅱ）∵，

∴当时，；当时，.

∴当时，取得极小值，

即（）.

（Ⅲ）解法一：∵，所以

又，

∴，

令，则.

∵在单调递增，∴，

∵，，

∴存在使得.

∵在单调递增，

∴当时，；当时，，

即在单调递增，在单调递减，

∴，

又∵，，，

∴当时，取得最小值.

解法二： ∵，所以

又，

∴，

令，

则，

当时，

，又因为，所以，，

所以，所以.

又，，

∴当时，取得最小值.

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

1

题型：单选题

|

单选题 · 5 分

12．已知定义在上的可导函数满足：，则与（是自然对数的底数）的大小关系是（）

A>

B<

C

D不确定

正确答案

A

解析

知识点

导数的运算

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点