- 数列与不等式的综合
- 共132题
22.给定数列









(1)对于数列:3,4,7,1,求出相应的
(2)若







①设

②若数列




正确答案
(1)
(2)①证明略;②
解析
(1)当

同理可得
(2)①当


当
两式相减得

所以,数列


②由①知:
又
由于
所以由
所以

因为

由

但




考查方向
本题考查数列的综合应用,突出考查考查推理论证与抽象思维的能力,是难题.数列的综合应用在近几年各省市的高考试卷中频频出现,是高考的热点问题,往往以等差数列、等比数列为载体,涉及递推公式、通项公式、前项和,结合数列单调性、数列恒成立等知识交汇命题.
解题思路
题(1),当


题(2)①,利用等比数列的定义证明











题(2)②,由①得到





易错点
对含有






知识点
32.已知两个无穷数列






(1)若数列

(2)若数列





①若数列

②若数列






正确答案
an=2n-1; 



解析
(1)数列


∴

(2)①∵数列



∴数列

故
② ∵

而数列



假设存在正整数





i.当
当



ii.当
显然不存在

iii.当
当


所以
当




此时



考查方向
本题主要考查数列的综合运算
解题思路
1、求出an,bn;
2、利用定义求解,即可得到结果。
易错点
本题易在利用新定义求解时发生错误。
知识点
18.设数列{an}的前n项和为Sn,己知a1=l,nan+1=(n+2)Sn,n∈N*.求证:
正确答案
(1)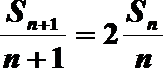
(2)略.
解析
本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
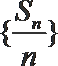
(2)由上知

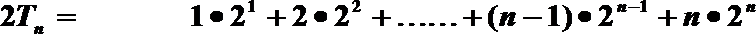
①-②得: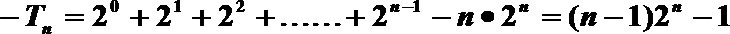

考查方向
本题考查了数列的问题.属于高考中的高频考点。
易错点
错位相减法求和时相减的结果项数易错。
知识点
22.已知数列



(1)若


(2)设





(3)设







正确答案
(1)
(2)详见解析
(3)
解析
因为



故

(3)因为

当

当

所以
因为


①当

②当




③当






综上,

知识点
12.数列{an}的通项公式为an =
①{an}为先减后增数列;
②{an}为递减数列:
③
④
其中正确命题的序号为
正确答案
解析
先取对数得
由此可知an的单调性与
故此先研究
构造函数

所以
由此可知

又因
所以
因此函数
故{an}为递减数列,
且
故选C。
考查方向
本题主要考查了数列的单调性与有界性
解题思路
首先取对数得



易错点
对于数列单调性无从下手。
知识点
17. 设数列




(1)求数列
(2)求数列



正确答案
(1)
(2)略
解析
(1)由已知

即
从而

又因为



所以数列



(2)由(1)得



因为



即
考查方向
解题思路
第一问直接利用
易错点
1、第一问中不能把
2、第二问中右边端点通过求和就能证明,但是左边端点不能想到结合函数的单调性来解决。
知识点
16.已知等差数列





(1)
(2)
(3)
(4)当

(5)
其中正确的有 (把你认为正确的说法都写上)
正确答案
(1)(2)(4)
解析
由
















考查方向
本题主要考查了函数与数列的联系及等差数列的公式与性质。
易错点
不知道如何处理这个式子
知识点
20.若实数数列



(1)若数列




(2) 求证:若数列


(3) 若数列






正确答案
(1)
(2)见解析
(3)
解析
(1)因为

所以
所以
所以

所以
(2) 假设


所以

故

假设

则

故

(3)由(Ⅱ)可知

且最多连续两项都是负数,最多连续三项都是正数.
因此存在最小的正整数


设


故有

由上可知


因为
所以当

当



记


当



此时

若


此时

当



综上可知

考查方向
本题主要考察了数列中项的问题,属于难题,是高考的热点,解决此类题的关键:是会对数列中的项进行分析。
易错点
1、本题易在对数列中的项分析不全面出现错误 。
2、对数列中项的性质研究不全面出现错误。
知识点
20.某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树.在下图里,你可以看到规划种植果树的列数(
(1)按此规律,



(2)定义:


正确答案
(1)


(2)当

解析
(1)


(2)

当

松树增加的速度快,
当

果树增加的速度快.
考查方向
本题主要考查归纳法求数列的通项公式,考查观察能力、归纳能力和即时学习能力.
解题思路
对题(1),可以通过观察、归纳得到通项公式;
对题(2),后项与前项作差比大小即可.
易错点
寻找各图中增加树木之间的关联容易出错,对新定义的概念不容易理解.
知识点
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列

(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
正确答案
(1)
当


当





(2)当

当
由

即
解得

解析
本题属于数列的应用题,题目的难度是中等,本题的关键是:
(1)、从所给的数列中找出规律,并求出两数列的通项公式;
(2)、再根据数列的通项公式的分段函数性质,求出各自的前n项和,最后利用函数的性质给出答案。这类数列的应用题型较为常见。
考查方向
本题考查了数列与函数之间的综合应用,特别是分段函数与数列的应用
易错点
1、分类讨论:



知识点
扫码查看完整答案与解析



































