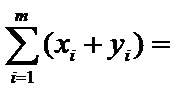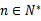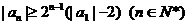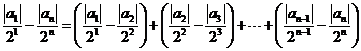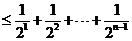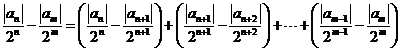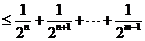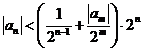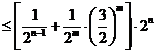- 数列与不等式的综合
- 共132题
某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30)
正确答案
知识点
12.已知函数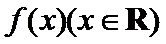
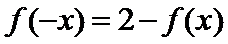
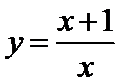
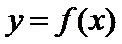
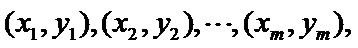
正确答案
知识点
设数列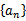
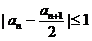
(Ⅰ)求证:
(Ⅱ)若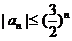
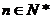
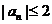
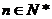
正确答案
(I)由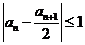
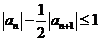
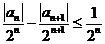

所以
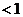
因此
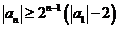
(II)任取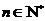
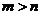
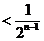
故
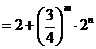
从而对于任意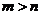
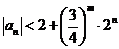
由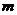
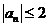
否则,存在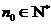
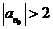
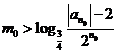
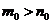
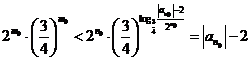
与①式矛盾.
综上,对于任意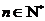
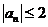
知识点
已知





27.证明:数列{
28.若对一切



正确答案
令



而对于

若


若


因此,在区间








故数列


解析
见答案
考查方向
解题思路
由题

易错点
字母太多,导致感觉混乱没有思路;
正确答案
解析
对一切


设



当



当



因为



因此


故实数a的取值范围是
考查方向
解题思路
由题问题等价于



易错点
不会构造函数
17.在等比数列






正确答案
(1)


(2)由题意知:
∴
∴
解析
(1)具体的分析如下:



(2)由题意知:
∴
∴
∴
考查方向
等比数列的通项公式,裂项相消法求和.
解题思路
先求出bn,然后用裂项相消求和
易错点
分类讨论p=1和p不等1时候的情况
知识点
17.设





(Ⅰ)求数列
(Ⅱ)若数列



正确答案
证明,(Ⅰ)因为
当

两式相减,得
即
所以当

所以
因为

(Ⅱ)因为


所以
所以

因为

因为

所以

所以当


所以
解析
本题属于数列应用中的基本问题,两问难度相当,(I)直接按照步骤来求(II)要裂项相消求和即可.
考查方向
本题考查了数列的相关知识点:
1、利用递推公式推导通项公式;
2、数列中的关系;
3、利用递推公式求解通项公式要单独把n=1拿出来验证;
4、数列中常用的求和方法----裂项法。
解题思路
易错点
知识点
15.已知数列


(Ⅰ)求数列
(Ⅱ)设



正确答案
(Ⅰ)
解析
解:设等比数列

因为

所以
即
解得
所以
(Ⅱ)证明:因为
所以数列


所以

考查方向
解题思路
本题主要考查考等差、等比数列的概念和性质及方程思想,解题思路如下:1、由条件











易错点
本题第二问直接把数列
知识点
(16分)(2015•上海)已知数列{an}与{bn}满足an+1﹣an=2(bn+1﹣bn),n∈N*.
(1)若bn=3n+5,且a1=1,求数列{an}的通项公式;
(2)设{an}的第n0项是最大项,即a
(3)设a1=λ<0,bn=λn(n∈N*),求λ的取值范围,使得{an}有最大值M与最小值m,且
正确答案
1)解:∵an+1﹣an=2(bn+1﹣bn),bn=3n+5,
∴an+1﹣an=2(bn+1﹣bn)=2(3n+8﹣3n﹣5)=6,
∴{an}是等差数列,首项为a1=1,公差为6,
则an=1+(n﹣1)×6=6n﹣5;
(2)∵an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=2(bn﹣bn﹣1)+2(bn﹣1﹣bn﹣2)+…+2(b2﹣b1)+a1
=2bn+a1﹣2b1,
∴
∴
∴数列{bn}的第n0项是最大项;
(3)由(2)可得
①当﹣1<λ<0时,


∴
∴λ∈
∴
②当λ=﹣1时,a2n=3,a2n﹣1=﹣1,
∴M=3,m=﹣1,

③当λ<﹣1时,当n→+∞时,a2n→+∞,无最大值;
当n→+∞时,a2n﹣1→﹣∞,无最小值.
综上所述,λ∈(﹣
知识点
已知函数




(1)求证:数列
(2) 若




(3)若



正确答案
(1) 证:由题意
即
∴
∴
∵常数


∴数列


(2) 当


所以
因为

因而最小值为
(3) 由(1)知,


即

当



当




∵
∴当

∴

∴
综上所述,存在实数
解析
本题属于数列与不等式的综合应用题,题目的难度是偏难,本题的关键是:
(1)、利函数的性质求出数列的通项公式;
(2)、利用等比数列的求和公式求出前n项和的表达式,并求出最小值;
(3)、根据数学归纳法,分类讨论出k的取值范围。
考查方向
本题考查了数列的综合应用题,特别是数列与不等式之间的应用题
易错点
1、由


知识点
18.设数列{an}的前n项和为Sn,己知a1=l,nan+1=(n+2)Sn,n∈N*.
(1)求证:
(2)设Tn= S1+S2+--+Sn,求证:(n+l) Tn<nSn+1.
正确答案
(1)
(2)略.
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
所以
(2)由上知


①-②得:
即(n+l) Tn<nSn+1.
考查方向
本题考查了数列的问题.属于高考中的高频考点。
解题思路
本题考查数列问题,解题步骤如下:
(1)利用等比数列的定义证明。
(2)利用错位相减法求和。
易错点
错位相减法求和时相减的结果项数易错。
知识点
扫码查看完整答案与解析