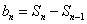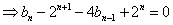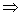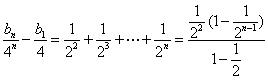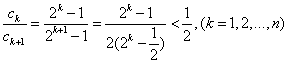- 数列与不等式的综合
- 共132题
已知等比数列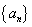
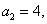
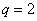
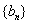
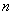
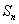
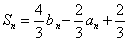

(1)求数列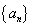
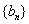
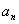
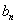
(2)设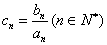
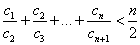
正确答案
见解析。
解析
(1) 解法一:由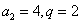
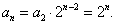
由上式结合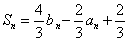
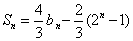
则当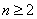
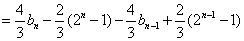
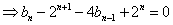
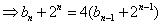
∵
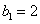
∴数列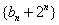
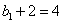
∴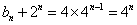
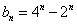
【解法二:由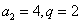
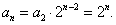
由上式结合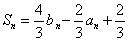
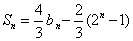
则当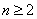
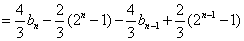
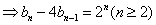
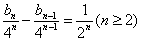
∴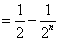
∵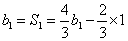
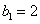
∴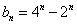
(2) 由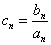
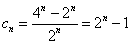
【或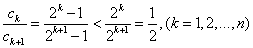
∴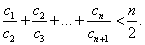
知识点
设等差数列





(1) 若



(2) 若

正确答案
见解析。
解析
知识点
已知正项数列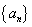
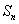
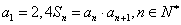
(1)求数列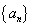
(2)设数列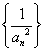

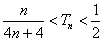
正确答案
见解析。
解析
知识点
设函数



(1)求函数
(2)当

(3)设



正确答案
见解析。
解析
(1)显然


令
ⅰ)当




ⅱ)当




在区间



(2)ⅰ)


ⅱ)

于是:

由(1)可知

即证明不等式

(法一)由上可知:不等式

若

故
即当


故当


(法二)令



由表


即

由于

故函数

又当

于是指数函数

同理当

于是指数函数

于是,当

从而函数



易知当


当


又易知

综上,当



(3)证法一:令


则不等式
注意到:




于是

故
从而


故原不等式
证法二:同上可将不等式

即



又
故
于是

又

知识点
已知数列{




(1)求

(2)设



正确答案
见解析。
解析
知识点
扫码查看完整答案与解析