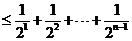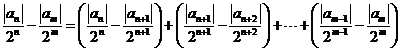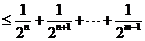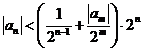- 数列与不等式的综合
- 共132题
某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30)
正确答案
知识点
12.已知函数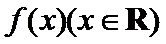
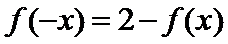
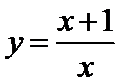
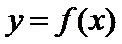
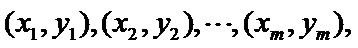
正确答案
知识点
设数列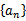
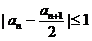
(Ⅰ)求证:
(Ⅱ)若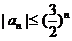
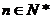
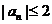
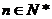
正确答案
(I)由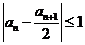
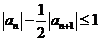
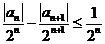

所以
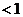
因此
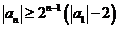
(II)任取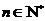
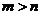
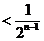
故
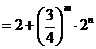
从而对于任意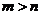
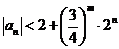
由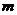
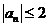
否则,存在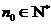
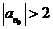
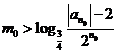
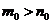
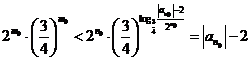
与①式矛盾.
综上,对于任意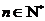
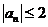
知识点
已知





27.证明:数列{
28.若对一切



正确答案
令



而对于

若


若


因此,在区间








故数列


解析
见答案
考查方向
解题思路
由题

易错点
字母太多,导致感觉混乱没有思路;
正确答案
解析
对一切


设



当



当



因为



因此


故实数a的取值范围是
考查方向
解题思路
由题问题等价于



易错点
不会构造函数
(16分)(2015•上海)已知数列{an}与{bn}满足an+1﹣an=2(bn+1﹣bn),n∈N*.
(1)若bn=3n+5,且a1=1,求数列{an}的通项公式;
(2)设{an}的第n0项是最大项,即a
(3)设a1=λ<0,bn=λn(n∈N*),求λ的取值范围,使得{an}有最大值M与最小值m,且
正确答案
1)解:∵an+1﹣an=2(bn+1﹣bn),bn=3n+5,
∴an+1﹣an=2(bn+1﹣bn)=2(3n+8﹣3n﹣5)=6,
∴{an}是等差数列,首项为a1=1,公差为6,
则an=1+(n﹣1)×6=6n﹣5;
(2)∵an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=2(bn﹣bn﹣1)+2(bn﹣1﹣bn﹣2)+…+2(b2﹣b1)+a1
=2bn+a1﹣2b1,
∴
∴
∴数列{bn}的第n0项是最大项;
(3)由(2)可得
①当﹣1<λ<0时,


∴
∴λ∈
∴
②当λ=﹣1时,a2n=3,a2n﹣1=﹣1,
∴M=3,m=﹣1,

③当λ<﹣1时,当n→+∞时,a2n→+∞,无最大值;
当n→+∞时,a2n﹣1→﹣∞,无最小值.
综上所述,λ∈(﹣
知识点
扫码查看完整答案与解析