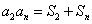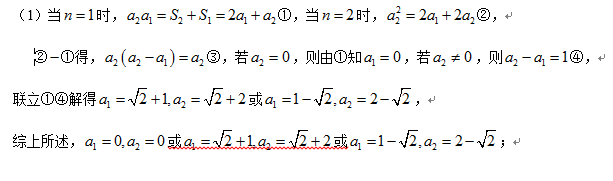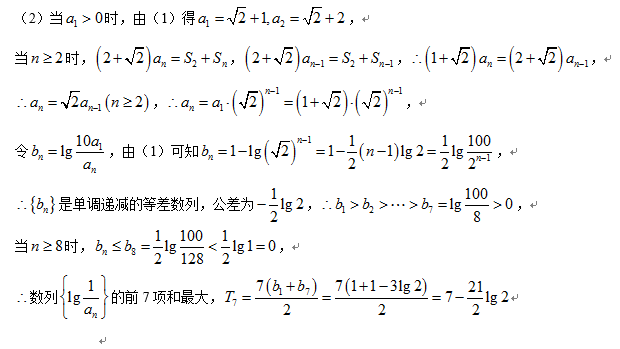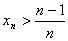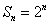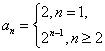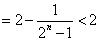- 数列与不等式的综合
- 共132题
已知各项为正的数列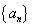
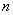
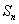
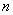
(1)求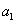
(2)求数列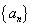
(3)若数列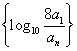
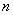
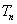
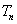
正确答案
见解析。
解析
解:
知识点
已知正项数列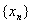
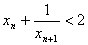
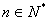
(1)证明:
(2)证明: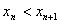
(3)证明: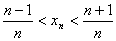
正确答案
见解析。
解析
(1)
方法一:因为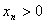
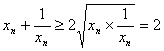
故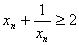
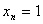
方法二:
因为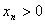
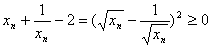
故
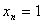
(2)由(1)知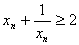

所以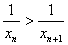
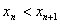
(3)先证:
当n=1时,不等式显然成立;
假设当n=k(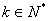
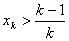
当n=k+1时,由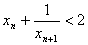
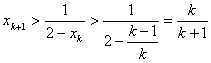
即当n=k+1时,不等式成立;
综上,对一切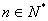
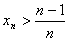
再证:
由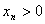
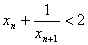
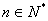
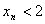
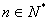
所以当n=1时,不等式显然成立;
当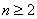
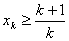
则有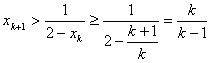
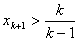
所以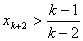
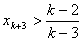
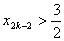
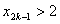
与题设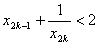
所以对一切
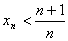
所以对一切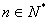
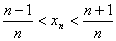
知识点
已知数列



(1)求数列

(2)设


(3)设

正确答案
见解析。
解析
(1)由题意,当

两式相减得

由

所以对一切正整数n,有
故

(2)由(1),得
所以
①两边同乘以

①-②,得
所以
故
(3)由(1),得

知识点
正项数列
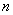

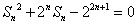
(1)求数列
(2)令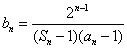
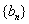
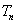
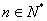
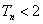
正确答案
见解析
解析
(1)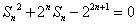
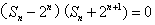
当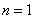
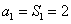
当
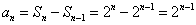
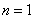
(2)当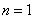
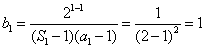
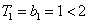
当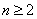
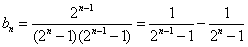
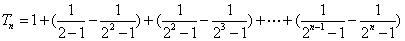
综上,对于任意的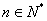
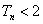
知识点
设an是函数f(x)=x3+n2x﹣1(n∈N+)的零点。
(1)证明:0<an<1;
(2)证明:
正确答案
见解析。
解析
解:(1)∵f(0)=﹣1<0,f(1)=n2>0,且f(x)在R上的图象是一条连续曲线,
∴f(x)在(0,1)内有零点,
∵f′(x)=3x2+n2>0,∴f(x)在(0,1)上是增函数,f(x)在(0,1)内只有一个零点,
而an是函数f(x)=x3+n2x﹣1(n∈N+)的零点,
∴0<an<1;
(2)先证明左边的不等式,因an3+n2an﹣1=0,由(1)知0<an<1,
∴a

∴an>



∵an>


∴a1+a2+…+an>1﹣






再证明右边的不等式,由于f(





∴

由(1)知,0<an<1,且an3+n2an﹣1=0,
∴an=
∵当n≥2时,a1+a2+…+an<










∴当n∈N*时,a1+a2+…+an<
综上,
知识点
扫码查看完整答案与解析