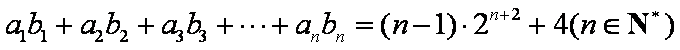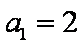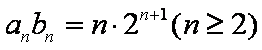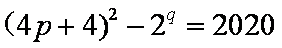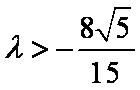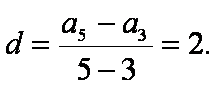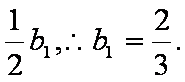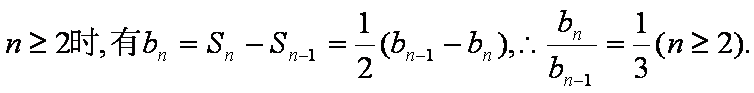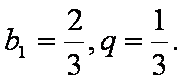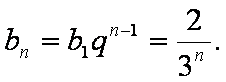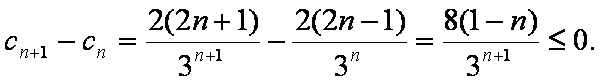- 数列与不等式的综合
- 共132题
已知数列
(1)求证:数列

(2)若
正确答案
(1)
解析
解析:(1)
故数列{bn}是等差数列 ………………………………3分

(2)由(1)

又Sn是递增的,Sn的最小值是

知识点
已知数列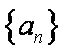
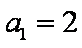


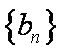

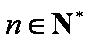
(1)求数列
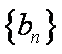
(2)是否存在
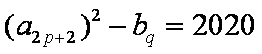
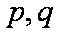
(3)是否存在非零整数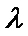

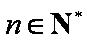
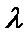
正确答案
见解析
解析
(1)法1:设数列
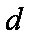


因为
令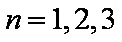

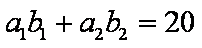
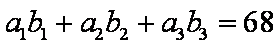
所以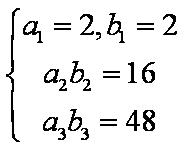
得
经检验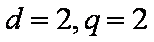
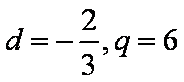
所以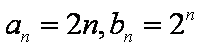
法2:因为
对任意的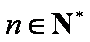
则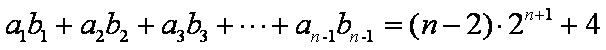

①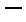
又
由于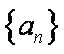

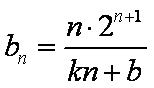
因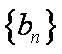

即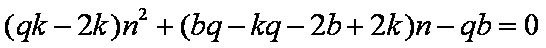
所以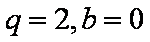
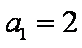
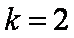

(2)解:假设存在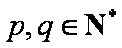
化简得
由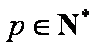
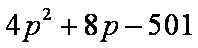
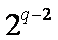
得
故
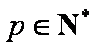
(3)由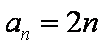
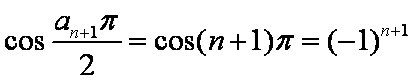
设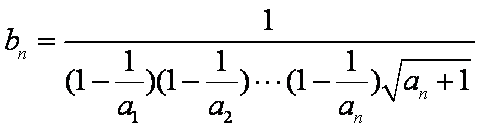
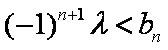
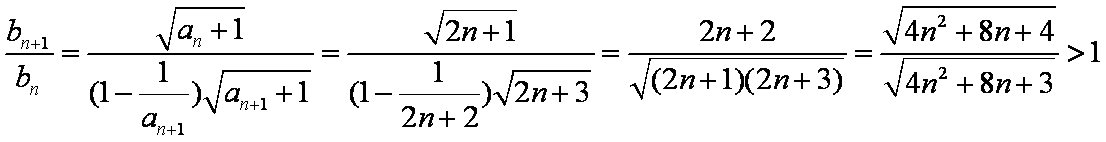
∵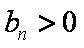
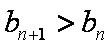

假设存在这样的实数


① 当
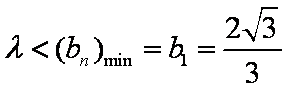
② 当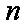
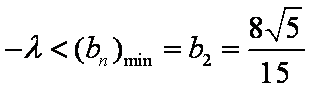
综上,
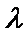
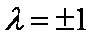
知识点
已知数列


(1)求数列

(2)设数列





正确答案
见解析
解析
(1)依题意得
解得

又数列


(2)令
∴

由 



则
知识点
已知等差数列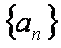
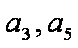
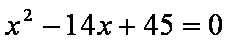
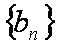
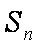

(1)求数列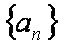
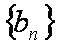
(2)记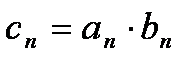
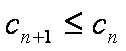
正确答案
见解析
解析
解:(1)∵a3,a5是方程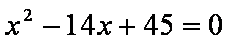
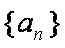
∴a3=5,a5=9,公差
∴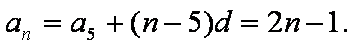
又当n=1时,有b1=S1=1-
当
∴数列{bn}是等比数列,
∴
(2)由(1)知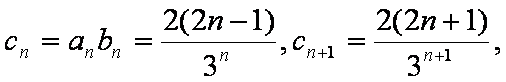
∴
∴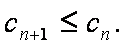
知识点
设等差数列



(1)求数列
(2)设



正确答案
见解析
解析
(1)方法一:设等差数列

又

故
方法二:


(2)方法一:由已知可得
相加得
又


则

方法二:设



由题意得
则

知识点
数列






(1)求数列

(2)设


正确答案
见解析
解析
解析:(1)当

又





得


所以数列

(2)由(1)可得

知识点
20.若由数列




(I)在数列


(II)若数列
(III)若数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知曲线








(1)求

(2)令

(3)若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(1)求数列
(2)数列



(3)设各项均不为零的数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知曲线






(1)求
(2)求证:
(3)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析