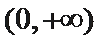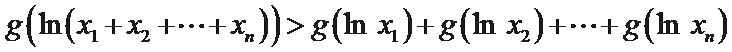- 数列与不等式的综合
- 共132题
20.已知
(I)求证:数列{an,-1)是等比数列;
(Ⅱ)当n取何值时,bn取最大值,并求出最大值;
(Ⅲ)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 数列



(1)求数列
(2) 记




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数f(x)(x∈D),若x∈D时,恒有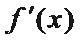
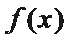
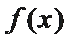
(Ⅰ)当函数f(x)=m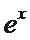
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与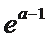
正确答案
解:(Ⅰ)由
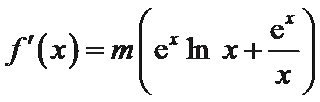
因为函数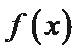
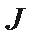
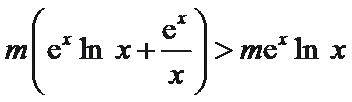
即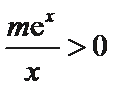
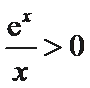
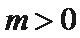
即
(Ⅱ)①构造函数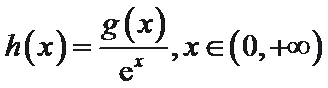
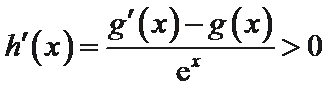
可得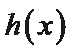
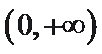
当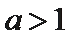
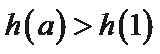
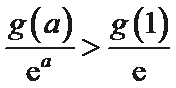
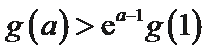
当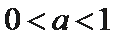
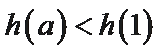
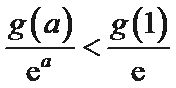
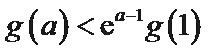
当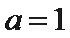
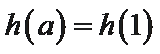
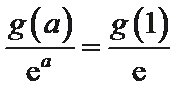
②因为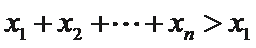
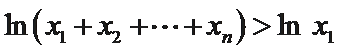
由①可知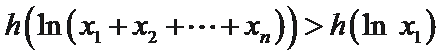

整理得
同理可得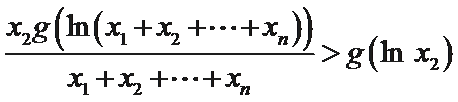
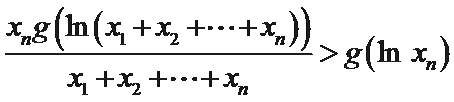
把上面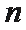
可得
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}中,a1=t(t∈R,且t≠0,1),a2=t2,且当x=t时,函数f(x)=
(Ⅰ)求证:数列{an+1-an}是等比数列;
(Ⅱ)若bn=anln|an|(n∈N),求数列{bn}的前n项和Sn;
(Ⅲ)当t=-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}的前n项和为Sn,Sn=2
(1)求证:数列
(2)设数列{ 2nan}的前n项和为Tn,An=




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析