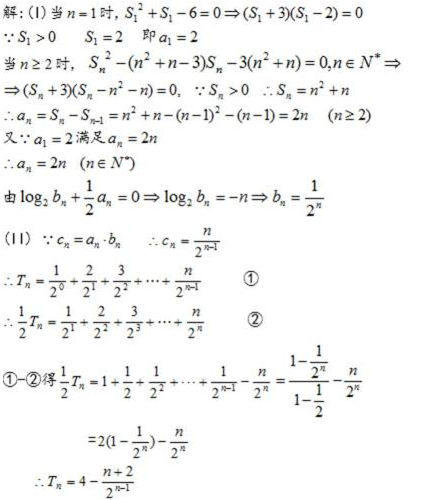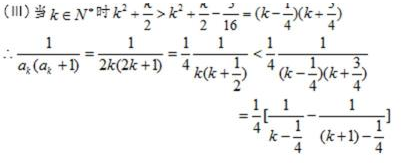- 数列与不等式的综合
- 共132题
19.已知数列




(1)求数列
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)求证:
(2)记


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设各项为正数的数列

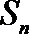

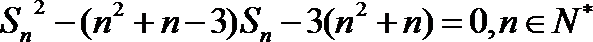
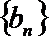
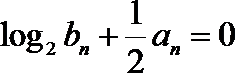
(Ⅰ)求数列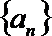
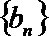
(Ⅱ)设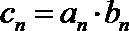
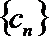

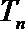
(Ⅲ) 证明:对一切正整数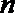
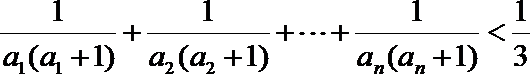
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列
(1)求数列

(2)若存在


正确答案
解:(1)
(2)
由(1)可知当
设
则
又

所以所求实数
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数集





(1)分别判断数集


(2)求


(3)由(2)及通过对

正确答案
(1)由于



由于








(2)∵




从而
当




从而



故数列
(3)命题一:对于一切大于或等于3的奇数


证明:由(2),不妨设





因为







第1组:

第2组:

第3组:

第


上一组的第2项总大于下一组的第1项,再注意到
第1组的各数从左到右依次为:
第2组的各数从左到右依次为:
第3组的各数从左到右依次为:
第

于是,有
由(﹡),




成等比数列.
命题二:对于一切大于或等于6的偶数


证略(同命题一的证明类似)
命题三:对于一切





(证略)若学生指出:当


例如数列

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析