- 数列与不等式的综合
- 共132题
1
题型:简答题
|
22.用数学归纳法证明: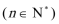
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
数列与不等式的综合数学归纳法的应用
1
题型:填空题
|
9.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
数列与不等式的综合等差数列与等比数列的综合
1
题型:
单选题
|
4.若数列




正确答案
B
解析
依题意可得bn+1=pbn,则数列

知识点
等比数列的判断与证明等比数列的性质及应用数列与不等式的综合
1
题型:填空题
|
8.已知数列{bn}中,bn+1=

正确答案
4与0
解析
由b1=0,得
所以
当n为奇数时, 
则当n=1时,b1=0最小,
同时,最大值不存在,无限的趋近于1.
当n为偶数时, 
则当n=2时,b2=2最大,
此时,最小值不存在,无限的趋近于1.
综上可知,数列{bn}的最大项为b2=4,最小项为b1=0.
知识点
由递推关系式求数列的通项公式数列与不等式的综合
1
题型:
单选题
|
10.已知数列 (n∈N*)满足

正确答案
C
解析
由于t<a1<t+1,
得a2=a1-t,
易得0<a1-t<1,
即0<a2<1,又t>2,
那么a3=t+2-a2=2t+2-a1,
又t+1<2t+2-a1<t+2,
即
又1<t+2-a1<2,
即1<a4<2,
得a4<t,
从而a5=t+2-a4=a1,
结合
可得实数k的最小值为4.
知识点
由递推关系式求数列的通项公式数列与不等式的综合
下一知识点 : 数列与向量的综合
扫码查看完整答案与解析