- 导数及其应用
- 共2569题
5.如下流程图所示的程序,如果输出i=3,则x的最小值为( )
正确答案
解析
运行流程图,由于输出i=3.所以i=1时,





知识点
设实数


正确答案
14
解析
画出约束条件

知识点
2.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)当


(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(Ⅰ)设曲线


(Ⅱ)当


(Ⅲ)令




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
17. 已知函数
(Ⅰ)若


(II)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(I)求函数
(II)设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(I)求实数
(II)求

(III)对任意给定的正实数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1) 求函数
(2) 若函数






(3) 求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)求
(Ⅱ)当





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:定义在R上的函数
(1)若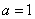
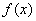
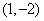
(2)若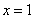
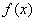
(3)若函数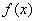

正确答案
解:(1)当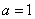
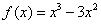
则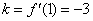
∴切线方程: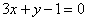
(2)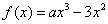
∵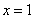
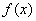
∴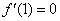
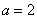
(3)①当a=0时,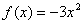
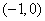
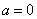
②当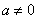
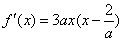
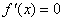
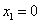
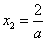
当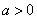
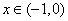
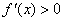
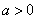
当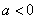
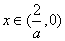

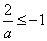

综上所述,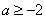
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析