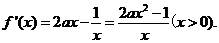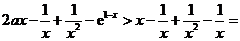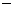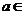导数及其应用_章节学习

1

题型：填空题

|

填空题 · 12 分

已知函数.

（I）当时，求曲线在处的切线方程；

(II)若当时，，求的取值范围.

正确答案

（I）的定义域为.当时，

，曲线在处的切线方程为

（II）当时，等价于

令，则

，

（i）当，时，，故在上单调递增，因此；

（ii）当时，令得

，

由和得，故当时，，在单调递减，因此.

综上，的取值范围是

知识点

导数的几何意义导数的运算利用导数求参数的取值范围

1

题型：单选题

|

单选题 · 5 分

已知a函数f(x)=x3-12x的极小值点，则a=（　　　）

A-4

B-2

C4

D2

正确答案

D

知识点

导数的几何意义利用导数求函数的极值

1

题型：简答题

|

简答题 · 12 分

20. 已知函数.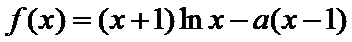

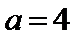
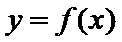
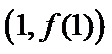
（I）当时，求曲线在处的切线方程；

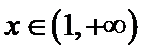
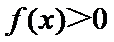
(II)若当时，，求的取值范围.

正确答案

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式

1

题型：单选题

|

单选题 · 5 分

设直线l1，l2分别是函数f(x)= 图象上点P1，P2处的切线，l1与l2垂直相交于点P，且l1，l2分别与y轴相交于点A，B则则△PAB的面积的取值范围是

A(0,1)

B(0,2)

C(0,+∞)

D(1,+ ∞)

正确答案

A

知识点

导数的几何意义

1

题型：填空题

|

填空题 · 17 分

21．已知函数 ,，（，为常数）

（Ⅰ）若在处的切线过点，求的值；

（Ⅱ）设函数的导函数为，若关于的方程有唯一解，求实数的取值范围；

（Ⅲ）令，若函数存在极值，且所有极值之和大于，求实数的取值范围。

正确答案

（Ⅰ）；

（Ⅱ）；

（Ⅲ）

解析

本题属于导数的基本问题，题目的难度是逐渐由易到难，

（1）直接按步骤来求，

（2）要注意分离参数；

（3）要注意讨论。

（1）设在处的切线方程为，

因为，

且，所以，

切线方程为，即，

当，，将代入，得。

（2），

由题意，得有唯一解，

即方程有唯一解，

令，

则，

所以在区间，上是增函数，在区间是减函数，又，，故实数的取值范围是

（3）因为，所以，

因为存在极值，

所以在上有根，即在上有根，则有．

显然，当时，不存在极值（舍），即方程有两个不等正根，记方程的两个根为，

则，解得①；

又因为

，解得②；

由①②，得所求实数的取值范围是

考查方向

【考查方向】本题主要考查了导数的应用，导数的应用主要分以下几类：

1．利用导数的几何意义求切线方程，

2．利用导数研究函数的单调性、极值和最值或零点，

3．利用导数研究不等式恒成立或存在性。

易错点

1.第二问中，易忽视分离参数；

2.第三问中，易忽视“”的讨论．

知识点

导数的几何意义利用导数求函数的极值利用导数求参数的取值范围

1

题型：单选题

|

单选题 · 5 分

4．设曲线上任一点处切线斜率为，则函数的部分图象可以为（）

A

B

C

D

正确答案

C

解析

由题可知，g(x)=cosx,所以易得：A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查导数的几何意义

解题思路

（1）求出k；（2）判断图像，即可得到结果。

A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

本题易在求k时发生错误。

知识点

知图选式与知式选图问题导数的几何意义

1

题型：简答题

|

简答题 · 12 分

21．已知函数（其中，是自然对数的底数），为导函数．

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）若，试证明：对任意，恒成立．

正确答案

见解析

解析

本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求；（2）要注意对参数的讨论．

（Ⅰ）由得，，所以曲线在点处的切线斜率为，，

曲线切线方程为，即．

（Ⅱ）由，得，令，所以，，因此，对任意，等价于，

由，，得，，

因此，当时，，单调递增；时，，单调递减，

所以的最大值为，故，

设，，所以时，，单调递增，，故时，，即，

所以．

因此，对任意，恒成立．

考查方向

本题考查了利用导数的几何意义和综合应用，分类讨论，讨论点大体可以分成以下几类：

（1）根据判别式讨论；

（2）根据二次函数的根的大小；

（3）定义域由限制时，根据定义域的隐含条件；

（4）求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论；

（5）多次求导求解等．

解题思路

本题考查导数的几何意义和综合应用，解题步骤如下：

（1）求导，然后求切线方程。

（2）对参数分类讨论证得结论。

易错点

第二问中的易丢对x的分类讨论。

知识点

导数的几何意义利用导数证明不等式

1

题型：简答题

|

简答题 · 12 分

21．已知函数（为常数），其图象是曲线．

（1）当时，求函数的单调减区间；

（2）设函数的导函数为，若存在唯一的实数，使得与同时成立，求实数的取值范围；

（3）已知点为曲线上的动点，在点处作曲线的切线与曲线交于另一点，在点处作曲线的切线，设切线的斜率分别为．问：是否存在常数，使得？若存在，求出的值；若不存在，请说明理由．

正确答案

（1）；

（2）；

（3）当时，存在常数，使得；当时，不存在常数使得．

解析

（1）当时，．令，解得，

的单调减区间为．

（2），由题意知消去，得有唯一解．令，则，以在区间，上是增函数，在上是减函数，又，，故实数的取值范围是．

（3）设，则点处切线方程为，

与曲线：联立方程组，得，即，所以点的横坐标．由题意知，，，若存在常数，使得，则，即常数使得，所以，解得．故当时，存在常数，使得；当时，不存在常数使得．

考查方向

本题考查了利用导数研究函数的单调性；利用导数研究曲线上某点切线方程

解题思路

（1）先求原函数的导数，根据f′（x）＜0求得的区间是单调减区间，即可；

（2）由于存在唯一的实数x0，使得f（x0）=x0与f′（x0）=0同时成立，则

存在唯一的实数根x0，就把问题转化为求函数最值问题；（3）假设存在常数λ，依据曲线C在点A处的切线l1与曲线C交于另一点B，曲线C在点B处的切线l2，得到关于λ的方程，有解则存在，无解则不存在．

易错点

第二问中的方程根的问题转化成最值问题

知识点

导数的几何意义利用导数研究函数的单调性利用导数求参数的取值范围

1

题型：填空题

|

填空题 · 5 分

16.已知曲线x在点(1，1)处的切线与曲线y=ax2+ (a+2)x+l相切，则a= .

正确答案

6

解析

y=x+lnx的导数为y′=1+1/x，曲线y=x+lnx在x=1处的切线斜率为k=2，

则曲线y=x+lnx在x=1处的切线方程为y-1=2x-2，即y=2x-1．由于切线与曲线y=ax2+（a+2）x+1相切，故y=ax2+（a+2）x+1可联立y=2x-1，得ax2+ax+2=0，又a≠0，两线相切有一切点，所以有△=a2-8a=0，解得a=8．故答案为：8．

考查方向

曲线的切线方程，导数的几何意义

解题思路

先求出曲线在切点处的切线方程，然后联立成方程组，化成一元二次方程，利用根的判别式求解。

易错点

导数的几何意义理解的不透彻，不会求切点。

知识点

导数的几何意义

1

题型：填空题

|

填空题 · 5 分

13．已知函数的图象在点处的切线方程是，则．

正确答案

7

解析

由题可知：k=f’(2)=1,f(2)=6，所以7．

考查方向

本题主要考查了导数的几何意义

解题思路

本题考查导数的几何意义，解题思路如下：利用导数的几何意义求出f’(2);利用切线方程求解。

易错点

本题必须注意导数的几何意义

知识点

导数的几何意义导数的运算

1

题型：填空题

|

填空题 · 14 分

设函数f(x)=ax2－a－lnx，g(x)=－，其中a∈R，e=2.718…为自然对数的底数。

（Ⅰ）讨论f(x)的单调性；

（Ⅱ）证明：当x＞1时，g(x)＞0；

（Ⅲ）确定a的所有可能取值，使得f(x)＞g(x)在区间（1，+∞）内恒成立。

正确答案

（I）

<0，在内单调递减.

由=0，有.

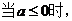
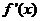
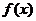
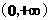
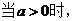
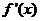
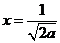
当时，<0，单调递减；

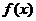
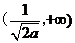
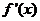
当时，>0，单调递增.

（II）令=，则=.

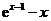
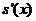
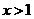
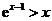
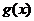
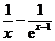
当时，>0，所以，从而=>0.

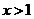
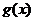
（iii）由（II），当时，>0.

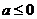
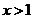
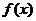
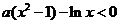
当，时，=.

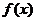
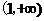
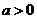
故当>在区间内恒成立时，必有.

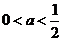
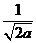
当时，>1.

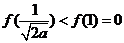
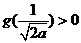
由（I）有,从而，

所以此时>在区间内不恒成立.

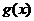
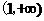
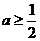
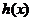
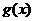
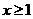
当时，令=().

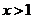
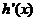
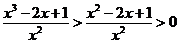
当时，=.

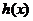
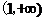
因此在区间单调递增.

又因为=0，所以当时，=>0，即>恒成立.

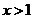
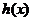
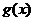
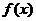
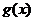
综上，.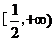

知识点

导数的几何意义利用导数研究函数的单调性利用导数求参数的取值范围

1

题型：简答题

|

简答题 · 16 分

19．已知函数在处的切线方程为.

（1）求的值；

（2）若对任意的，都有成立，求的取值范围；

（3）若函数的两个零点为，试判断的正负，并说明理由.

正确答案

（1）

（2）

（3）．

解析

试题分析：本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求（2）要注意对参数的讨论（3）涉及恒成立问题，转化成求函数的最值，这种思路是一般解法，往往要利用“分离参数法”．涉及对数函数，要特别注意函数的定义域．

（1）由题意得，因函数在处的切线方程为，

所以，得.

（2）由（1）知对任意都成立，

所以，即对任意都成立，从而.

又不等式整理可得，令，

所以，得，

当时，，函数在上单调递增，

同理，函数在上单调递减，所以，

综上所述，实数的取值范围是.

（3）结论是.

证明：由题意知函数，所以，

易得函数在单调递增，在上单调递减，所以只需证明即可.

因为是函数的两个零点，所以，相减得，

不妨令，则，则，所以，，

即证，即证，

因为，所以在上单调递增，所以，

综上所述，函数总满足成立.

考查方向

本题考查了利用导数的几何意义，利用导数求含参数的函数单调区间，分类讨论讨论点大体可以分成以下几类：

1、根据判别式讨论；

2、根据二次函数的根的大小；

3、定义域由限制时，根据定义域的隐含条件；

4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论；

5、多次求导求解等．

解题思路

本题考查导数的性质，解题步骤如下：

1、求导，然后解导数不等式，算极值。

2、对参数分类讨论求得单调区间。

3、涉及恒成立问题，转化成求函数的最值，利用“分离参数法”

易错点

1、第二问中恒成立问题，转化为求函数的最值，最值如何求解。

2、第三问中构造函数不正确得不到正确结论。

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数求参数的取值范围

1

题型：填空题

|

填空题 · 5 分

16.函数在点处的切线斜率的取到最小值时相应切线的倾斜角为。

正确答案

解析

因为，∴，所以，当且仅当时取等号，即时，取得最小值为，相应切线的倾斜角为。

考查方向

本题主要考查了导数的几何意义，基本不等式．

解题思路

先求导，再利用基本不等式来求解。

易错点

导数的几何意义不清楚。

知识点

导数的几何意义导数的运算

1

题型：填空题

|

填空题 · 5 分

14.已知函数f(x)=ax3+x+1的图像在点（1，f(1)）处的切线过点（2,7），则a= .

正确答案

1

知识点

导数的几何意义

1

题型：填空题

|

填空题 · 5 分

16.已知为偶函数，当时，，则曲线在点处的切线方程式_____________________________.

正确答案

解析

当时，，则．又因为为偶函数，所以，所以，则切线斜率为，所以切线方程为，即．

考查方向

本题主要考查了函数的奇偶性、解析式、导数的几何意义等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

由当时，，则．又因为为偶函数，则切线斜率为，所以切线方程为，即

易错点

对函数的奇偶性、解析式、导数的几何意义理解出现错误、计算错误

知识点

导数的几何意义

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点