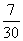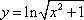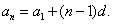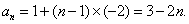- 导数及其应用
- 共2569题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
从甲、乙等10位同学中任选3位去参加某项活动，则所选3位中有甲但没有乙的概率为
正确答案
解析
10选3共有
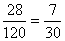
知识点
已知两曲线参数方程分别为
正确答案
解析
又因为
知识点
下列函数为偶函数的是( )
Ay＝sin x
By＝x3
Cy＝ex
D
正确答案
解析
∵函数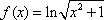
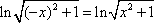
∴f(x)是偶函数
知识点
设单位向量m＝(x，y)，b＝(2，－1)，若m⊥b，则|x＋2y|＝__________.
正确答案
解析
因为m⊥b，所以m·b＝2x－y＝0.①
又因为m为单位向量，
所以x2＋y2＝1.②
由①②解得
所以|x＋2y|＝
知识点
已知向量a＝(x－1,2)，b＝(2,1)，则a⊥b的充要条件是( )
A
Bx＝－1
Cx＝5
Dx＝0
正确答案
解析
∵a＝(x－1,2)，b＝(2,1)，a⊥b，∴a·b＝(x－1，2)·(2,1)＝2(x－1)＋2×1＝2x＝0，即x＝0
知识点
若向量
A
B
C
D
正确答案
解析
因为
知识点
设
（1）求
（2）讨论
（3）求
正确答案
(1)1
(2)
（3）
解析
（1）由题设知
∴
当
当
因此，
所以
(2)
设
当
当
因此，
当
即
（3）由（1）知
即
知识点
已知事件“在矩形ABCD的边CD上随机取一点P，使△APB的最大边是AB”发生的概率为
A
B
C
D
正确答案
解析
知识点
已知等差数列{an}中，a1=1，a3=-3。
（1）求数列{an}的通项公式；
（2）若数列{an}的前k项和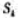
正确答案
（1）
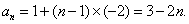
解析
（1）设等差数列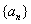
由
解得d=-2。
从而，
（2）由（1）可知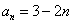
所以
进而由
即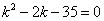
又
知识点
在一组样本数据（x1，y1），（x2，y2），…，（xn，yn）（n≥2，x1,x2,…,xn不全相等）的散点图中，若所有样本点（xi，yi）(i=1,2,…,n)都在直线
A－1
B0
C
D1
正确答案
解析
有题设知，这组样本数据完全正相关，故其相关系数为1，故选D.
知识点
设
则
正确答案
解析
解析：∵
又∵
∴
联立①②，解得，
知识点
正确答案
解析
因
知识点
已知函数
(1)当
(2) 若
正确答案
（1）{
解析
(1)当
当
当2＜
当
∴
(2) 
当
∴
故满足条件的
知识点
已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是( )。
正确答案
解析
若x0是f(x)的极小值点，则y＝f(x)的图像大致如下图所示，则在(－∞，x0)上不单调，故C不正确
知识点
扫码查看完整答案与解析