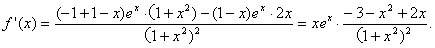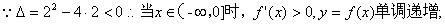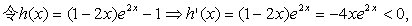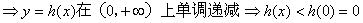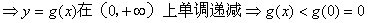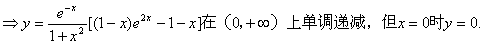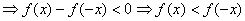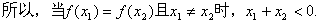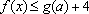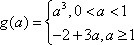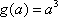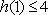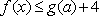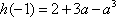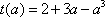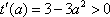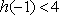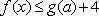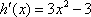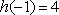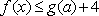- 导数及其应用
- 共2569题
已知函数f(x)=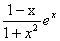
(1)求f(x)的单调区间;
(2)证明:当f(x1)=f(x2)(x1≠x2)时,x1+x2<0.
正确答案
见解析
解析
(1)
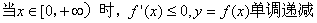
所以,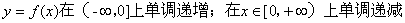
(2)由(1)知,只需要证明:当x>0时f(x) < f(-x)即可。
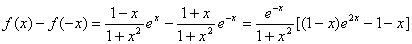
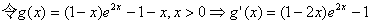
知识点
已知



正确答案
解析



知识点
(x+1/x)9的展开式中,x3的系数是_________
正确答案
84
解析
∵ 

知识点
已知函数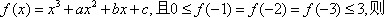
正确答案
解析
设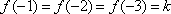
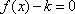
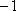
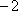
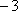
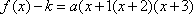
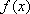
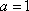
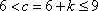
知识点
设




(1)求


(2)求数列{

正确答案
(1) 
(2)
解析
(1)

(2)
上式左右错位相减:

知识点
已知函数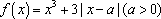
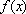
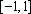
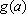
(1)求
(2)证明:当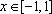
正确答案
见解析
解析
(1)解:因为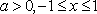
(ⅰ)当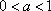
若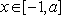
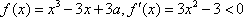
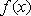
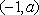
若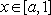
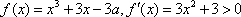
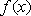

所以
(ⅱ)当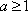
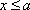
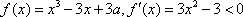
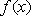
综上,
(2)证明:令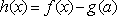
(ⅰ)当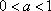
若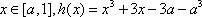
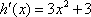
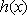
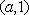
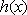
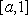
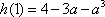
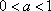
故
若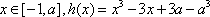
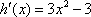
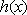
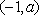
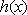
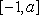
令
则
知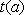
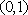
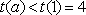
故
(ⅱ)当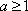
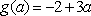
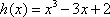
此时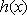
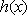
故
综上,当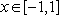
知识点
观察下列等式:
…
照此规律, 第n个等式可为().
正确答案
解析
考察规律的观察、概况能力,注意项数,开始值和结束值。
第n个等式可为:
知识点
在平面直角坐标系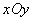
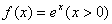
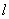
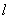
正确答案
解析
略
知识点
x为实数,



正确答案
解析
函数


知识点
已知函数

正确答案
解析



















知识点
已知角




正确答案
解析
略
知识点
若实数


正确答案
4
解析
略
知识点
在平面直角坐标系下,曲线



正确答案


解析
化为普通方程后,圆心到直线的距离小于或等于圆的半径(
知识点
在等差数列



正确答案
2;
解析
略
知识点
已知




正确答案
-1
解析
略
知识点
扫码查看完整答案与解析