- 直线、圆及圆锥曲线的交汇问题
- 共263题
20.过圆




(1)求椭圆C的方程;
(2)若在椭圆上存在一点P,使得


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知







(Ⅰ)求
(Ⅱ)一动圆过点


(Ⅲ)过点





正确答案
解:(Ⅰ)

所以AC边所在直线的方程为

由


又
所以

(Ⅱ)设动圆圆心为



所以

故点



从而动圆圆心的轨迹方程

(Ⅲ)

由

故
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,

(1)求证:直线CD的斜率为定值;
(2)延长DC交x轴于点E,若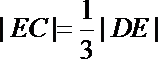

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,抛物线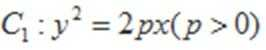
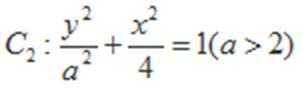
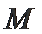
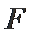
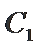
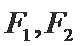
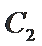
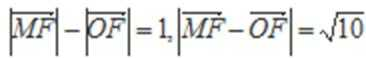
(1)求抛物线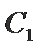

(2)是否存在经过M的直线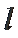
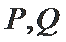
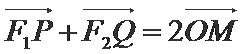
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆





(I)求椭圆方程;
(Ⅱ)若





(III)在(Ⅱ)的条件下,试问




正确答案
(I)



(Ⅱ)


直线


代入椭圆





(III)设存在


解析
解析已在路上飞奔,马上就到!
知识点
9. 在抛物线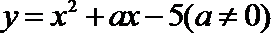
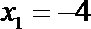
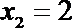
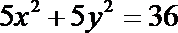
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:


(Ⅰ)求椭圆C的标准方程
(Ⅱ)若直线L:
求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.圆

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知圆C:




(Ⅰ)求椭圆E的方程;
(Ⅱ)求证:|AF|-|BF|=|BM|-|AM|.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知圆N:

(Ⅰ)当直线l的斜率为-1时,求线段AB的长;
(Ⅱ)设点M点N关于直线y=x对称,问是否存在直线l,使得

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


























