- 直线、圆及圆锥曲线的交汇问题
- 共263题
20.已知椭圆


(Ⅰ)求椭圆
(Ⅱ)已知直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 线段








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知以原点O为中心的椭圆,它的短轴长为



(Ⅰ)求椭圆的方程和离心率;
(Ⅱ)若
(Ⅲ)设


正确答案
(Ⅰ)解:由题意,可知椭圆的方程为
由已知得
解得
所以椭圆的方程为

(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为y=k(x-3).
联立方程组
依题意△=12(2-3k2)>0,得
设P(x1,y1),Q(x2,y2),则


由直线PQ的方程得为y1=k(x1-3),y2=k(x2-3),于是,
y1y2=k2(x1-3) (x2-3)= k2[x1x2-3(x1+ x2)+9]. ③
∵
由①②③④得5k2=1,从而
所以直线PQ的方程为

(理科做)
(Ⅲ)证明:∵P(x1,y1),Q(x2,y2), A(3,0),
∴



因为F(2,0), M(x1,-y1),故

而

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:+=1(a>b>0)的离心率e=,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为.
(1)求椭圆C的方程;
(2)过原点且斜率为的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C: 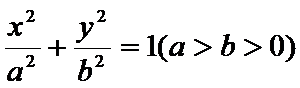
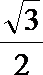
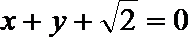
(1) 求椭圆C的方程;
(2) 设斜率不为零的直线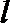
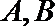
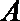
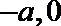
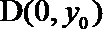
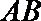
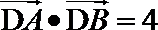
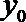
(3)若过点M(1,0)的直线与椭圆C相交于P, Q两点,如果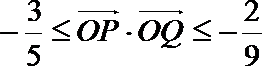
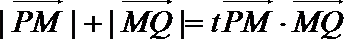
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知圆




(Ⅰ)求椭圆的方程;
(Ⅱ)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设






(1)对任意





(2)若点


(3)对(1)中点







正确答案
(1)直线






(2)若点


(方法1)两边同除以

∴点

(方法2) 设

得
即


(3)(方法1)设

由
① 当直线
设


②当直线
设



即原点到直线


∴直线

(方法2)设

则
即
注意到圆

∴
即原点到直线

∴直线

解析
解析已在路上飞奔,马上就到!
知识点
10.已知椭圆








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设椭圆






(1)求椭圆
(2)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆


(1)求椭圆的方程;
(2)设不过原点







正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

























