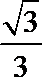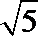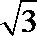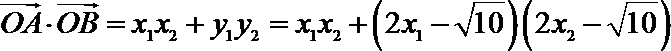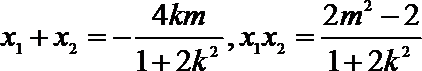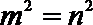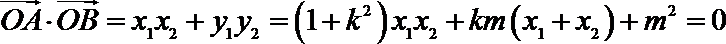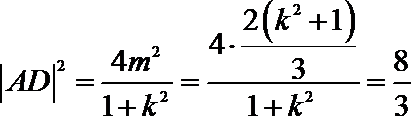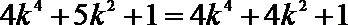- 直线、圆及圆锥曲线的交汇问题
- 共263题
18. 已知点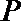
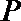
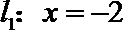
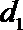
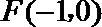
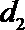
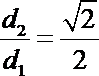
(1)求动点P所在曲线C的方程;
(2)直线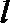
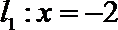
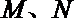
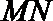
(3)记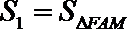
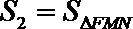
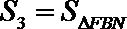
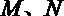
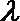
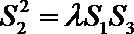
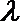
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知:向量

(1)求动点 M 的轨迹 C 的方程;
(2)已知直线







正确答案
解:设点
∵
∴
∴点 M 的轨迹C是以
∴
∴ 动点M 的轨迹 C的方程为
(2)
由(1)知,轨迹C是椭圆

设满足条件的直线



则直线

将①代入椭圆方程并整理得:


将②代入椭圆方程并整理得:

由△BDE是等腰直角三角形得
∴

∵方程④

∴即满足条件的直线

解析
解析已在路上飞奔,马上就到!
知识点
18. 在平面直角坐标系xOy中,椭圆C:

(1)求a,b的值。
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点。
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.抛物线y=x2与直线x-y+2=0构成封闭平面区域(含边界)为D.若曲线x2-2ax+y2-4y+a2+ 
正确答案
解析
曲线
即为
其圆心坐标为E(a,2),半径
由图可知,当
圆与点D有公共点;
当a<0时,要圆与点D有公共点,
只需圆心到直线l:x-y+2=0的距离
则a的最小值为-
知识点
8.抛物线y=x2与直线x-y+2=0构成封闭平面区域(含边界)为D.若曲线x2-2ax+y2-4y+a2+ 
正确答案
解析
曲线
即为
其圆心坐标为E(a,2),半径
由图可知,当
圆与点D有公共点;
当a<0时,要圆与点D有公共点,
只需圆心到直线l:x-y+2=0的距离
则a的最小值为-
知识点
6.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线 l,此直线与上述两条曲线的四个交点,自左向右顺次记为A,B,C,D,如果|AB|,|BC|,|CD|按此顺序构成一个等差数列,则直线l的斜率为( ).
正确答案
解析
由题意可知,圆P的圆心坐标为(0,2),半径为2,抛物线S的焦点为(0,2),准线方程为y=-2,画出图象如图所示,其中|BC|=4.由于|AB|,|BC|,|CD|成等差数列,所以|AB|+|CD|=8,所以|AB|+|BC|+|CD|=12,则所求问题等价于当过抛物线S的焦点的直线被抛物线所截得的线段的长度为12时,求直线的斜率.设A(x1,y1),D(x2,y2),过A,D分别向抛物线的准线作垂线,垂足分别为A',D'.根据抛物线定义得|AP|=|AA'|=y1+2,|DP|=|DD'|=y2+2,所以|AD|=|AP|+|DP|=y1+y2+4=12,得y1+y2=8.由题意可知,直线l的斜率存在,且不为0.设直线l的斜率为k(k≠0),则直线l的方程为y=kx+2,即x=

知识点
21.如图,焦距为2的椭圆E的两个顶点分别为



(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线
圆的内部,求实 数m的取值范围.
正确答案
解:
(Ⅰ)设椭圆E的标准方程为
∴



∴
(Ⅱ)设


消去y,得,
∴


∵原点O总在以PQ为直径的圆内,∴
又
由


故实数m的取值范围是
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,椭圆C:

(1) 求椭圆C及抛物线C1、C2的方程;
(2) 若动直线l与直线OP垂直,且与椭圆C交于不同两点M、N,已知点

正确答案
(1) 由题意得A(a,0),B(0,
∴ 抛物线C1的方程可设为
由
代入
∴ 椭圆方程为

(2)由题意可设直线l的方程为
由
由
设M(x1,y1),N(x2,y2),则
∵
∴
∵
∴ 当
解析
解析已在路上飞奔,马上就到!
知识点
10.过双曲线
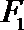
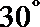
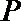
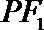
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知直线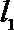
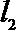
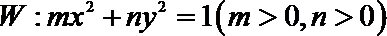
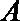

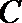
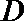

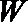
(1)若直线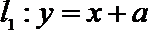

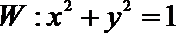
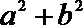
(2)若直线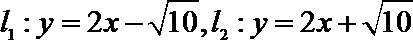
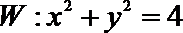
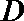

(3)求证:椭圆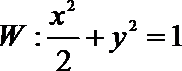
正确答案
(1)2;
(2)证明略;
(3)证明略,面积为
解析
(1)由于直线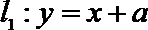
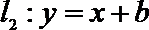

所以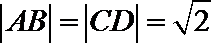
在等腰直角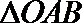
圆心

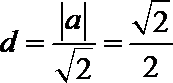
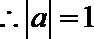
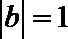

(2)由题知,直线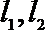
因为圆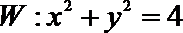

所以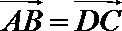
故四边形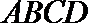
易知,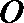
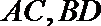
联立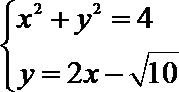
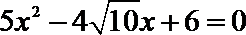
由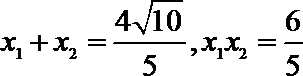
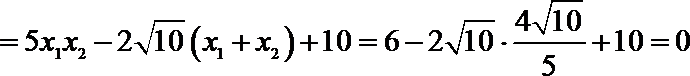
所以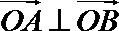
于是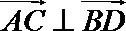
因为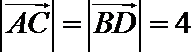
所以四边形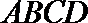
(3)证明:假设椭圆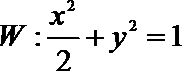
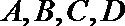
当直线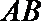
设直线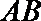
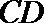
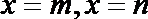
因为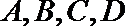
所以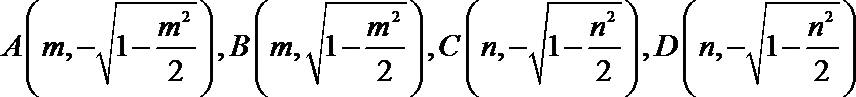
由四边形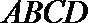
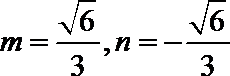
直线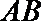
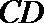
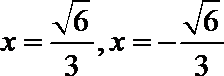
正方形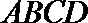

当直线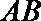
设直线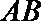
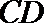
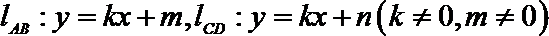
显然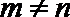
设
联立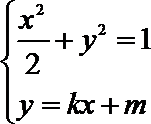
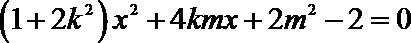
所以
代人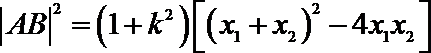
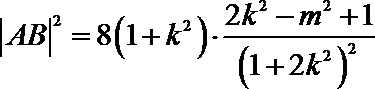
同理可得
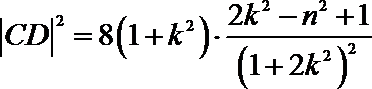
因为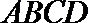
所以
解得
因为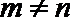
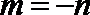
因此,直线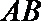
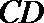
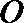
所以原点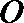
(由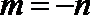
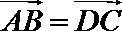

由
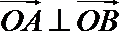
即
代人得
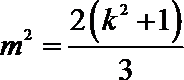
由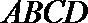

因为直线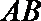
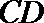
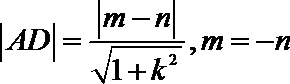
故
但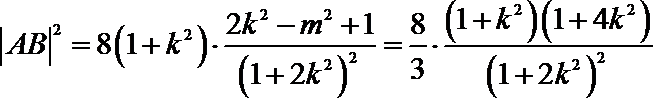
由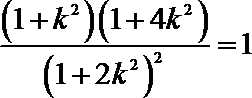
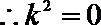

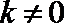
所以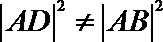
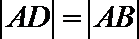
即当直线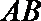
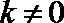
综上所述,椭圆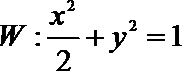
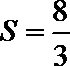
考查方向
本题主要考查直线与圆锥曲线的综合应用,考查学生分析问题解决问题的能力、逻辑推理能力,是难题.解析几何的综合应用在近几年各省市的高考试卷中频频出现,是高考的热点问题,往往以直线、圆、椭圆、双曲线、抛物线为载体,涉及各类曲线的定义与方程、各类曲线的性质,与曲线的轨迹方程的求解、直线与圆锥曲线的位置关系等知识交汇命题.
解题思路
题(1),先找到两直线分单位圆成长度相等的四段弧的位置,求得所截得的弦长,然后利用原点到直线距离公式求得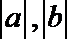
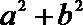
题(2),先证四边形
题(3),分类讨论说明椭圆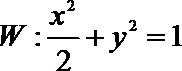
易错点
找不到直线与圆或者椭圆的正确的位置关系,从而无法解题.
知识点
扫码查看完整答案与解析