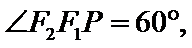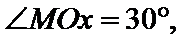- 直线、圆及圆锥曲线的交汇问题
- 共263题
15.已知圆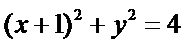

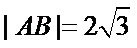
正确答案
8
解析
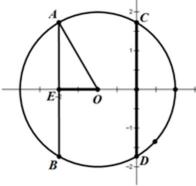
在平面直角坐标系中画出圆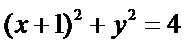
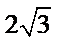
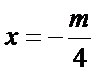
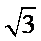
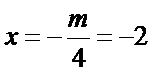
考查方向
解题思路
根据题意画出合适的图形,然后结合图形进行分析和计算.
易错点
本题必须要对抛物线的标准方程和几何性质有深刻的认识,否则容易因为误认为准线为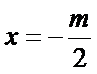
知识点
11. 已知双曲线




正确答案
解析
利用交点这一突破口,建立方程关系,进而求出a和c的关系,所以得到离心率为
考查方向
解题思路
先设交点坐标,与渐近线联立方程组,最后用余弦定理求得
易错点
计算错误、离心率、渐近线方程错误
知识点
11.双曲线
正确答案
解析
由题意得直线








考查方向
解题思路
1.先将直线
2.根据直线与圆相切得到
易错点
不会转化题中的条件:以A1A2为直径的圆内切于菱形F1B1F2B22.在由
知识点
15.已知圆


正确答案
8
解析
试题分析:由




考查方向
解题思路
由




易错点
对题所给条件不知如何应用导致本题没有思路。
知识点
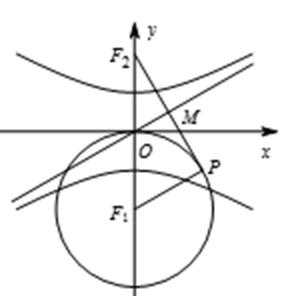
11.如图,已知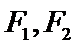
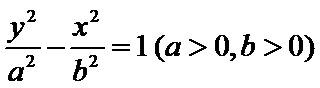
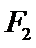
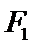
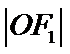
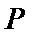
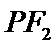
正确答案
解析
设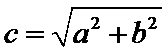
由题意得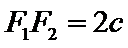
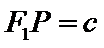
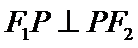
所以
因为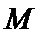
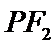
所以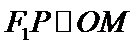
所以
所以
而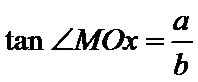
所以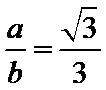
所以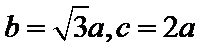
所以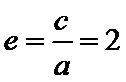
考查方向
解题思路
1、选根据题中条件求出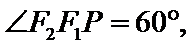
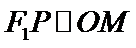
2.利用渐近线的斜率得到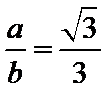
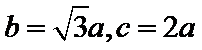
易错点
1、无法将题中条件准确转化;
2.焦点在y轴上的双曲线的渐近线的方程与焦点在x轴上的渐近线方程不同,此点容易出错。
知识点
20.在平面直角坐标系


(1)求椭圆C的方程;
(2)点P在椭圆C上,且在第一象限内,直线PQ与圆O:
正确答案
(1)
(2)
解析
试题分析:本题第(1)问属于椭圆简单几何性质的应用,是基础知识;第(2)问是直线与圆、椭圆的位置关系的问题,常用解析几何的基本思想方法求解,运算量比较大,需要考生在计算过程中认真、细心。解答过程如下:
(1)由
解得c=1,a=2, ∴

(2)法一:①当PM⊥x轴时,P

由
②当PM不垂直于x轴时,设

∵PQ与圆O相切,∴
∴
又

∴


综上:
法二:设


∵OP⊥OQ,∴OP·OQ=OM·PQ,
∴
∴
∴

∵


∴
考查方向
解题思路
1、第(1)问根据椭圆的标准方程以及几何性质,通过待定系数的方法即可求解;
2、第(2)问可以通过直线与圆的位置关系、直线垂直的条件,利用向量作为工具进行求解;
易错点
本题在解答第二问时往往会忽略考虑直线的斜率不存在的情况而导致错误的出现。
知识点
15.已知双曲线


正确答案
解析
双曲线










考查方向
本题主要考查双曲线的渐近线方程,直线与圆的位置关系,点到直线的距离公式等知识,意在考查考生运算求解能力和转化与化归的能力。
解题思路
1.先求出圆心到双曲线渐近线的距离;
2.利用点到直线的距离公式表示出
易错点
1.渐近线的方程求错;
2.不会数形结合由弦长转化为求点到直线的距离。
知识点
15.在平面直角坐标系







正确答案
解析
.
根据题意写出渐近线方程
所以
所以
考查方向
解题思路
该题思路比较清晰,主要有以下几个步骤1、求双曲线的渐近线2、根据圆的性质求出圆的方程3、渐近线与椭圆联立求出AB点坐标4、利用圆心到A的距离等于半径求出关系式
易错点
本题易错点主要集中在,1、渐近线的表达,2、外接圆的几何性质
知识点
正确答案
知识点
10.已知椭圆







正确答案
解析
设椭圆的点为




考查方向
本题主要考查了圆锥曲线的切线方程、面积计算和函数的最值问题,属于难度较大的题,常考求方程、离心率的值或范围、中点弦,面积等问题。
易错点
本题难在方程的合理假设与面积的计算易在集合的交并补运算上出问题。
知识点
扫码查看完整答案与解析