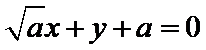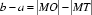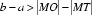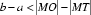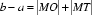直线、圆及圆锥曲线的交汇问题_章节学习

1

题型：单选题

|

单选题 · 5 分

设p：实数x，y满足(x–1)2–(y–1)2≤2，q：实数x，y满足则p是q的

A必要不充分条件

B充分不必要条件

C充要条件

D既不充分也不必要条件

正确答案

A

知识点

充要条件的应用直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 14 分

21．（本题满分14分）本题共2个小题，第1小题满分6分，第2小题满分8分

双曲线的左、右焦点分别为、，直线过且与双曲线交于两点

(1) 若的倾斜角为，是等边三角形，求双曲线的渐近线方程

(2) 设，若的斜率存在，且，求的斜率

正确答案

(1)由已知,

取，得

∵,

∴

即

∴

∴渐近线方程为

(2)若，则双曲线为

∴,

设, ，则

, ,

∴

(*)

∵

∴

∴代入(*)式，可得

直线的斜率存在，故

∴

设直线为，代入

得

∴，且

∴

∴直线的斜率为

知识点

双曲线的几何性质圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

在直角坐标系中，曲线C：y=与直线（＞0）交与M,N两点，

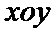
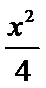
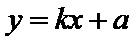
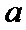
25.当k=0时，分别求C在点M和N处的切线方程；

26.y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）或

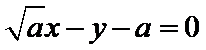
解析

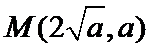
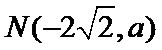
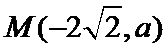
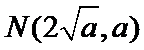
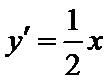
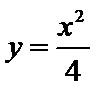
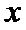
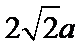
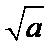
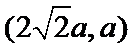
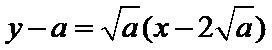
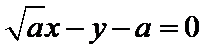
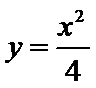
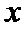
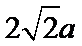
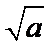
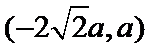
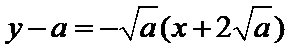
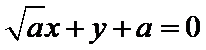
（Ⅰ）由题设可得，，或，.

∵，故在=处的到数值为，C在处的切线方程为

，即.故在=-处的到数值为-，C在处的切线方程为

，即.

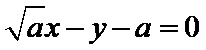
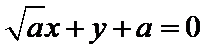
故所求切线方程为或.

考查方向

本题考查了抛物线的切线；直线与抛物线位置关系；探索新问题；运算求解能力。

解题思路

（Ⅰ）先求出M,N的坐标，再利用导数求出M,N.

易错点

本题在用导数求方程过程中易错

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）存在

解析

（Ⅱ）存在符合题意的点，证明如下：

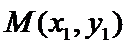
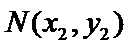
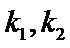
设P（0，b）为复合题意得点，，，直线PM，PN的斜率分别为.

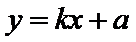
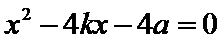
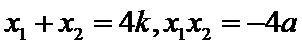
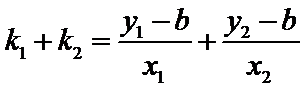
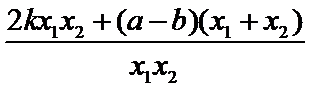
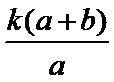
将代入C得方程整理得.

∴.

∴==.

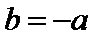
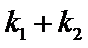
当时，有=0，则直线PM的倾斜角与直线PN的倾斜角互补，

故∠OPM=∠OPN，所以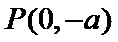符合题意.

考查方向

本题考查了抛物线的切线；直线与抛物线位置关系；探索新问题；运算求解能力。

解题思路

（Ⅱ）先作出判定，再利用设而不求思想即将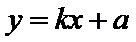代入曲线C的方程整理成关于的一元二次方程，设出M,N的坐标和P点坐标，利用设而不求思想，将直线PM，PN的斜率之和用表示出来，利用直线PM，PN的斜率为0,即可求出关系，从而找出适合条件的P点坐标.

易错点

本题在用导数求方程过程中易错，在直线和曲线的位置关系中易错。

1

题型：简答题

|

简答题 · 12 分

20.设圆的圆心为A，直线l过点B（1,0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

（I）证明为定值，并写出点E的轨迹方程；

（II）设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，求四边形MPNQ面积的取值范围.

正确答案

知识点

圆锥曲线中的范围、最值问题圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

1

题型：填空题

|

填空题 · 12 分

（本小题满分12分）

已知椭圆E:的焦点在轴上，A是E的左顶点，斜率为k(k>0)的直线交E于A,M两点，点N在E上，MA⊥NA.

（I）当t=4，时，求△AMN的面积；

（II）当时，求k的取值范围.

正确答案

（I）设，则由题意知，当时，的方程为，.

由已知及椭圆的对称性知，直线的倾斜角为.因此直线的方程为.

将代入得.解得或，所以.

因此的面积.

（II）由题意，，.

将直线的方程代入得.

由得，故.

由题设，直线的方程为，故同理可得，

由得，即.

当时上式不成立，

因此.等价于，

即.由此得，或，解得.

因此的取值范围是.

知识点

椭圆的定义及标准方程椭圆的几何性质圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

1

题型：填空题

|

填空题 · 13 分

（本小题满分13分）

已知椭圆E：的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l:y=-x+3与椭圆E有且只有一个公共点T.

（I）求椭圆E的方程及点T的坐标；

（II）设O是坐标原点，直线l’平行于OT,与椭圆E交于不同的两点A、B，且与直线l交于点P.证明：存在常数λ，使得∣PT∣2=λ∣PA∣·∣PB∣，并求λ的值.

正确答案

（I）由已知，，则椭圆E的方程为.

有方程组得.①

方程①的判别式为，由，得，

此方程①的解为，

所以椭圆E的方程为.

点T坐标为（2,1）.

（II）由已知可设直线的方程为，

有方程组可得

所以P点坐标为（），.

设点A，B的坐标分别为 .

由方程组可得.②

方程②的判别式为，由，解得.

由②得.

所以，

同理，

所以

.

故存在常数，使得.

知识点

椭圆的定义及标准方程椭圆的几何性质圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

20．已知抛物线的焦点，其准线与轴的交点为，过点的直线与交于两点，点关于轴的对称点为．

（Ⅰ）证明：点在直线上；

（Ⅱ）设，求内切圆的方程．

正确答案

见解析

解析

试题分析：本题属于圆锥曲线中的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求（2）要注意对参数的讨论．

（Ⅰ）由题可知，抛物线的方程为

则可设直线的方程为，，

故整理得，故

则直线的方程为即

令，得，所以在直线上．

（Ⅱ）由（Ⅰ）可知，所以，

又，

故，

则，故直线的方程为或

，

故直线的方程或，又为的平分线，

故可设圆心，到直线及的距离分别为

由

得或（舍去）．故圆的半径为

所以圆的方程为．

考查方向

本题考查了直线与圆锥曲线的位置关系及综合应用，属于高考中的高频考点．

解题思路

本题考查圆锥曲线与直线的位置关系，解题步骤如下：

1、利用e及对称性求a,b。

2、联立直线与椭圆方程求解。

易错点

第二问中表示直线斜率时容易出错。

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 14 分

19．已知椭圆C:的离心率为，点在椭圆C上。

（Ⅰ）求椭圆C的方程；

（Ⅱ）设动直线与椭圆C有且仅有一个公共点，判断是否存在以原点O为圆心的圆，满足此圆与相交两点，（两点均不在坐标轴上），且使得直线，的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由。

正确答案

（Ⅰ）；

（Ⅱ），．

解析

试题分析：本题属于解析几何的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求，（2）要注意直线不存在斜率的特殊情况，（3）要注意计算结果去正确性

（Ⅰ）解：由题意，得，，

又因为点在椭圆上，

所以，

解得，，，

所以椭圆C的方程为．

（Ⅱ）结论：存在符合条件的圆，且此圆的方程为．

证明如下：

假设存在符合条件的圆，并设此圆的方程为．

当直线的斜率存在时，设的方程为．

由方程组得，

因为直线与椭圆有且仅有一个公共点，

所以，即．

由方程组得，

则．

设，，则，，

设直线，的斜率分别为，，

所以

，

将代入上式，得．

要使得为定值，则，即，验证符合题意．

所以当圆的方程为时，圆与的交点满足为定值．

当直线的斜率不存在时，由题意知的方程为，

此时，圆与的交点也满足．

综上，当圆的方程为时，圆与的交点满足斜率之积为定值．

考查方向

本题主要考查了椭圆的标准方程、直线与椭圆的位置关系，直线与圆锥曲线的位置关系的考查主要分以下几类：

1．直线与圆锥曲线的公共点个数问题，

2．弦长问题，

3．中点弦问题．

解题思路

本题考查直线与椭圆的位置关系，解题步骤如下：

1．利用待定系数法求出椭圆的标准方程；

2．假设存在，设出圆的方程与直线方程；

3．联立直线与椭圆的方程，化简得到关于的一元二次方程，利用判别式为0求得的关系；

4．联立直线与圆的方程，化简得到关于的一元二次方程，利用平面向量的数量积求解；

5．讨论直线斜率不存在的情况，得到结论。

易错点

1、第二问中，联立直线与圆的方程得到关于关于的一元二次方程后，要注意验证判别式为正值；

2、第二问中，不要忘记“直线无斜率”的特殊情况。

知识点

椭圆的定义及标准方程圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

若圆与曲线的没有公共点，则半径的取值范围是

A B． C． D．

正确答案

A

考查方向

本题主要考查了圆与函数的综合应用，分式函数最值求法的应用等相关知识，意在考考生逻辑思维能力，运算求解能力，分析问题解决问题的能力，在近几年的各省高考题出现的频率较高，常与函数等知识点交汇命题，较难。

易错点

1、本题易在理解题意上出现错误。

知识点

直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

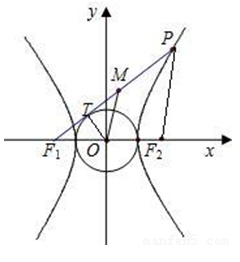
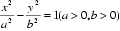
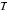
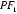
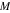
11．过双曲线的左焦点，作圆的切线交双曲线右支于点，切点为，的中点在第一象限，则以下结论正确的是（）

A

B

C

D

正确答案

A

解析

解：连OT，则OT⊥F1T，在直角三角形OTF1中，|F1T|=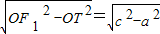=b．

连PF2，M为线段F1P的中点，

O为坐标原点∴OM=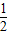PF2，

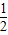
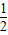
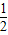
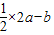
∴|MO|-|MT|=PF2-（ MF1-F1T）=（PF2-MF1）-b==a-b．

点评：本题主要考查双曲线的定义及三角形中位线和直线与圆相切时应用勾股定理．解答的关键是熟悉双曲线的定义的应用，直线与圆的位置关系以及三角形中的有关结论。B选项不正确，C选项不正确，D选项不正确，所以选A选项。

考查方向

本题主要考查双曲线与圆的知识

易错点

本题易在利用双曲线定义时发生错误。

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

知识点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

考查方向

易错点

知识点

正确答案

解析

考查方向

易错点

知识点