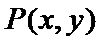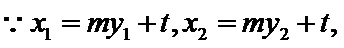- 直线、圆及圆锥曲线的交汇问题
- 共263题
8.过双曲线



正确答案
解析
设直线AC的方程为

由

由






考查方向
解题思路
设出过点


易错点
求直线与双曲线的渐近线交点时,发生错误。
知识点
14.已知抛物线





正确答案
2
解析
如图,由题意可得 AF=AC设AF=3m,由AB=2BC,可AB=2m,BC=m,过A作AD垂直x轴于D,设A的横坐标为


考查方向
解题思路
画出抛物线简图,用抛物线定义,结合题中的位置关系,数量关系,求出点A(2,2
易错点
对抛物线定义及性质掌握不熟
知识点
已知点

26.设椭圆的两个焦点分别为



27.若直线









正确答案


解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“


(Ⅰ)由题意可知,


因为


所以

易得椭圆的离心率
考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:
根据题意


本题第二问由“


易错点
未注意到点


正确答案
证明略.
解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“


(Ⅱ)由

因为直线



所以


设





显然直线





则

因为

所以
考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:
根据题意


本题第二问由“


易错点
未注意到点


如图,在平面直角坐标系xOy中,已知椭圆


23.求椭圆的标准方程;
24.过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
正确答案

解析
(1)由题意可得,e=

且c+

则b=1,即有椭圆方程为
考查方向
解题思路
(1)运用离心率公式和准线方程,可得a,c的方程,解得a,c,再由a,b,c的关系,可得b,进而得到椭圆方程;
易错点
本题考查椭圆的方程和性质,在应用几何意义时易错.
正确答案
y=x﹣1或y=﹣x+1.
解析
(2)当AB⊥x轴,AB=
当AB与x轴不垂直,设直线AB:y=k(x﹣1),A(x1,y1),B(x2,y2),
将AB方程代入椭圆方程可得(1+2k2)x2﹣4k2x+2(k2﹣1)=0,
则x1+x2=

则C(




若k=0,则AB的垂直平分线为y轴,与左准线平行,不合题意;
则k≠0,故PC:y+



从而|PC|=
由|PC|=2|AB|,可得

此时AB的方程为y=x﹣1或y=﹣x+1.
考查方向
解题思路
(2)讨论直线AB的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和弦长公式,以及两直线垂直的条件和中点坐标公式,即可得到所求直线的方程.
易错点
本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用韦达定理和弦长公式,计算易错.
已知椭圆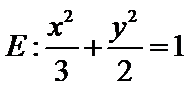
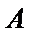
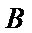
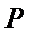
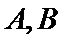
24.求直线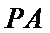
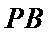

25.设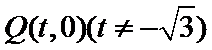

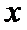
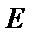

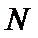
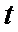
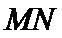
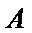

正确答案
直线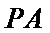
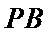
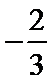
解析
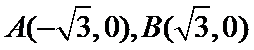
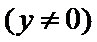
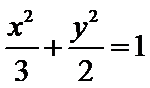
考查方向
解题思路
解题步骤如下:由椭圆的方程,可得到A ,B两点的坐标,设出点P(x,y),即可表示出直线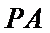
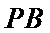
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
正确答案
存在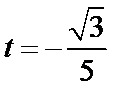
解析
【解析】令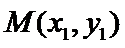
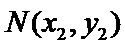
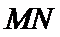
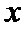
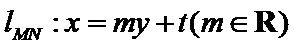
由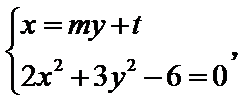
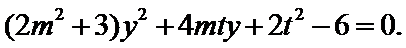
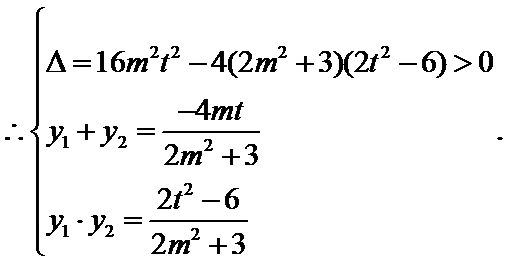
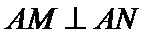
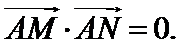
将(*)式代入上式,得
即
展开,得
整理,得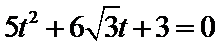
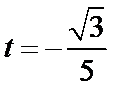
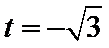
经检验,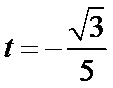
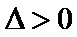
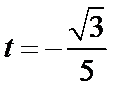
考查方向
解题思路
解题步骤如下:要满足以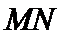
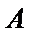

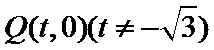
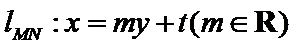
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
已知






24.求该椭圆的离心率;
25.设

正确答案
.e=
解析
当线段A


因为cos∠







考查方向
解题思路
先证出

易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
正确答案


解析
由24得椭圆方程为




则直线AC的方程为y=






(2) 若AB⊥x轴,则



综上所述,

考查方向
解题思路
由24得到含有b的椭圆方程,根据题意对直线AB、AC的斜率进行分为讨论,设出坐标,联立方程组,利用根与系数关系,结合向量关系式,将向量关系转化为坐标关系,用A的坐标及b,表求

易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
已知椭圆

25.求以线段
26.过点







正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

(I)因为


所以以线段

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

则直线



等价于
依题意,直线


由

因为直线


即

设





令

当

所以
化简得,
所以
当
所以存在点

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

已知抛物线


23.求抛物线C的方程;
24.已知动圆P的圆心在抛物线C上,且过定点D(0,4),若动圆P与x轴交于A、B两点,且

正确答案
(Ⅰ)
解析
(1) 设抛物线的焦点为

由








考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

正确答案

解析
设动圆圆心

且圆
令

解得:

当

当




所以

考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

7. 在平面直角坐标系中,双曲线




正确答案
解析
设双曲线的标准方程为
又因为点

所以,所求双曲线的标准方程我
考查方向
解题思路
采用待定系数法,由由双曲线的渐近线设标准方程
把点P代入方程求解,即可得到结果。
易错点
由双曲线的渐近线设标准方程出错
知识点
前间壁心肌梗死特征性心电图改变,见于
A.V3、V4、V5
B.V1、V2、V3、V4、V5
C.V1、V2、V3
D.V5、I、aVL
E.Ⅱ、Ⅲ、aVF
正确答案
C
解析
暂无解析
扫码查看完整答案与解析