- 直线、圆及圆锥曲线的交汇问题
- 共263题
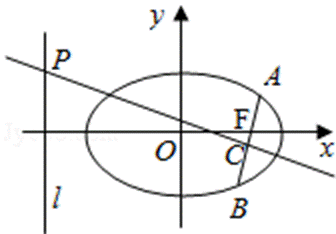
如图,在平面直角坐标系xOy中,已知椭圆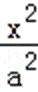
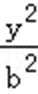

23.求椭圆的标准方程;
24.过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
正确答案
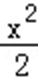
解析
(1)由题意可得,e=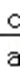

且c+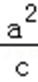
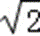
则b=1,即有椭圆方程为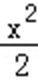
考查方向
解题思路
(1)运用离心率公式和准线方程,可得a,c的方程,解得a,c,再由a,b,c的关系,可得b,进而得到椭圆方程;
易错点
本题考查椭圆的方程和性质,在应用几何意义时易错.
正确答案
y=x﹣1或y=﹣x+1.
解析
(2)当AB⊥x轴,AB=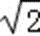
当AB与x轴不垂直,设直线AB:y=k(x﹣1),A(x1,y1),B(x2,y2),
将AB方程代入椭圆方程可得(1+2k2)x2﹣4k2x+2(k2﹣1)=0,
则x1+x2=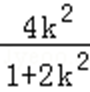
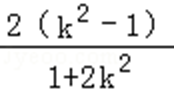
则C(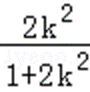
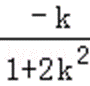
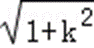

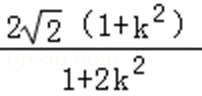
若k=0,则AB的垂直平分线为y轴,与左准线平行,不合题意;
则k≠0,故PC:y+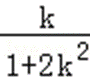
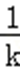
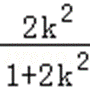
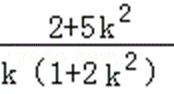
从而|PC|=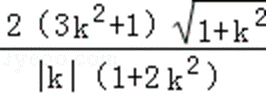
由|PC|=2|AB|,可得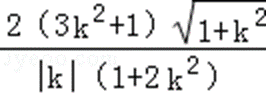
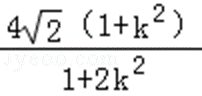
此时AB的方程为y=x﹣1或y=﹣x+1.
考查方向
解题思路
(2)讨论直线AB的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和弦长公式,以及两直线垂直的条件和中点坐标公式,即可得到所求直线的方程.
易错点
本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用韦达定理和弦长公式,计算易错.
在绿色新政潮的推波助澜下,气候问题和低碳经济已为世人关注,绿色壁垒再次成为世界贸易保护的手段。一些发达国家借环境保护之名,行贸易保护之实,说穿了就是“绿色贸易壁垒”,是发达国家对发展中国家的一种遏制。应对这种国际政治经济的竞争,我们要主动顺应绿色新政的潮流,大力发展低碳经济,实现绿色创新基础上的发展转型,走低能耗、低排放、低污染的可持续发展之路。 本段文字意在说明( )。
A.绿色新政潮引发贸易新壁垒
B.发达国家以环保为名实施贸易保护
C.我国要关注低碳经济
D.如何应对“绿色贸易壁垒”
正确答案
D
解析
[解析] 主旨推断题。文段前两句阐述了一个现实:在绿色新政潮的影响下,一些发达国家实行了“绿色贸易保护”;接下来就如何应对提出措施:要顺应绿色新政潮流,大力发展低碳经济。A项和B项是对背景现象的简单概括;C项是一项具体的应对措施,对文段内容的概括性较低。本题正确答案为D项。
选修4-4:坐标系与参数方程(本小题满分10分)
选做题:
在直角坐标系







31.求曲线
32.若曲线




正确答案
对于曲线




正确答案
联立曲线






市场营销组合的特点有( )
A.对企业来说都是“不可控因素”
B.是一个单一结构
C.是一个静态组合
D.要受企业市场定位战略的制约
正确答案
D
解析
暂无解析
大额可转让定期存单的特点主要有( )。
A.不记名
B.金额较大
C.一般比同期限的定期存款的利率高
D.利率既有固定的,也有浮动的
E.可以提前支取,也可以在二级市场上流通转让
正确答案
A,B,C,D
解析
[解析] 大额可转让定期存单的特点有:不记名;金额较大;利率既有固定的,也有浮动的,一般比同期限的定期存款的利率高;不能提前支取,但是可以在二级市场上流通转让。
金融市场的功能可以从微观和宏观两个方面来考察,下列属于宏观经济功能的是( )。
A.交易功能
B.反映功能
C.集聚功能
D.调节功能
E.资源配置功能
正确答案
B,D,E
解析
[解析] 金融市场的宏观经济功能是:资源配置功能、调节功能和反映功能。选项AC属于金融市场的微观经济功能。
已知抛物线





23.求抛物线
24.与圆






正确答案
设
则点



同理,点



两式结合,说明直线



由已知直线


故所求抛物线的方程为
解析
详见解题过程.
考查方向
本题考查抛物线的标准方程,直线与抛物线的关系.
解题思路
先设出点A,B的坐标,进而写出抛物线的切线方程,进而可以写出直线AB的方程,对照已知条件中直线的斜率即可求出p,进而可以写出抛物线的方程;
易错点
若不能根据直线AB的特征写出AB的方程,则可能导致思路受阻.
教师点评
本题把直线与抛物线相切融入到抛物线方程的求解中,命题形式灵活,具有较好的代表性.
正确答案
直线



所以

与抛物线方程联立,即
化简消






设


由

又点


解析
注意向量运算与坐标之间的互相转化.
考查方向
本题考查直线与圆的位置关系,直线与抛物线的关系.
解题思路
先根据直线与圆的相切求出m与k的关系,再把直线与抛物线联立,利用向量的运算及判别式即可求出结论.
易错点
忽略判别式容易导致错误
教师点评
本题具有一定的综合性,对计算能力有较高要求.
若椭圆





24.求椭圆的离心率;
25.过点





(2)【答案】设直线

∵


由(1)知,
由


∴

由①②知,
∵
∴
当且仅当



又当

∴由


正确答案
(1)由题意知,


解析
(1)由题意知,


考查方向
本题考查椭圆与抛物线的应用问题,主要涉及到两者焦距、焦点问题
解题思路
由题意,可知
易错点
线段的定比分点计算容易出错,离心率公式容易记错
教师点评
本题是椭圆焦距与抛物线焦点坐标的综合题,属于简单题,只要掌握线段定比分点的性质即可,在近几年中考到的频率较高,是解析几何中重要的一块
正确答案
直线方程为

椭圆方程为
解析
设直线

∵


由(1)知,
由


∴

由①②知,
∵
∴
当且仅当



又当

∴由


考查方向
本题考查椭圆中三角形面积最大问题,主要涉及到直线与椭圆的焦点问题、向量在椭圆中的应用问题以及函数值域问题
解题思路
先设出直线方程,联立椭圆方程和直线方程,利用韦达定理,求出两根和积,再利用向量坐标运算,求出关系式,列出面积公式,利用均值不等式求出直线方程和椭圆方程
易错点
计算容易出错,不容易想到均值不等式
教师点评
本题是向量、曲线相交与均值不等式的综合应用题,是一道难度较大的题型,需要掌握直线的不同设法、设而不求法、向量运算与面积问题、均值不等式在最值问题上会经常使用,值得注意
定期存款较股票型基金产品有一定特点,下列说法正确的是( )。
A.流动性高;收益率高
B.流动性高;收益率低
C.流动性低;收益率低
D.流动性低;收益率高
正确答案
C
解析
[解析] 一般说来,定期存款低于股票型基金产品的收益率,流动性也低于股票型基金产品。
根据《城镇职工基本医疗保险定点零售药店管理暂行办法》,定点零售药店须
A.经统筹地区药品监督管理部门审查,并经劳动保障行政部门确定
B.经统筹地区劳动保障行政部门审查,并经社会保险经办机构确定
C.经统筹地区劳动保障行政部门审查,并经药品监督管理部门确定
D.经统筹地区卫生行政部门审查,并经劳动保障行政部门确定
E.经统筹地区卫生行政部门审查,并经药品监督管理部门确定
正确答案
B
解析
暂无解析
扫码查看完整答案与解析