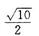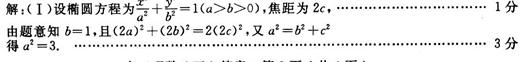直线、圆及圆锥曲线的交汇问题
共263题

· 直线、圆及圆锥曲线的交汇问题

直线、圆及圆锥曲线的交汇问题
共263题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

已知椭圆与双曲线有公共焦点，过椭圆C的右顶点B任意作直线，设直线交抛物线于P、Q两点，且

（1）求椭圆C的方程；

（2）在椭圆C上，是否存在点R(m，n)，使得直线与圆相交于不同的两点M、N，且△OMN的面积最大？若存在，求出点R的坐标及对应的△OMN的面积；若不存在，请说明理由。

正确答案

见解析。

解析

知识点

椭圆的定义及标准方程圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 14 分

已知抛物线：，直线与抛物线交于、不同两点，且。

（1）求抛物线的焦点坐标和准线方程；

（2）设直线为线段的中垂线，请判断直线是否恒过定点？若是，请求出定点坐标；若不是，说明理由；

（3）记点、在轴上的射影分别为、，记曲线是以为直径的圆，当直线与曲线的相离时，求的取值范围。

正确答案

见解析。

解析

（1）抛物线的焦点坐标为，准线方程为：

（2）设，，∵、是不同的两点，∴且不与轴垂直

∵，∴，，∴中点的坐标为

∴…

讨论：当时，直线的斜率，∴直线的方程为：，即，令得，即直线恒过定点

当时，直线的方程为：，也过点，故恒过定点

（3）由第（2）问可设直线的方程为：，即

联立，消去得，所以即，所以

所以以为直径的圆的方程为

当直线与曲线相离时，圆心到直线的距离，即

所以，即，即，

所有，即，所以或

又，且，所以或，即，或，或，或，

的范围为

知识点

抛物线的标准方程和几何性质圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 5 分

过双曲线的左焦点，作圆的切线，切点为E，延长EF交双曲线右支于点P，若E是FP的中点，则双曲线的离心率为__________.

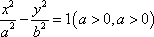
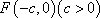
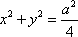
正确答案

解析

略

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 12 分

已知椭圆过点（0，1），其长轴、焦距和短轴的长的平方依次成等差数列.直线轴正半轴和y轴分别交于Q、P，与椭圆分别交于点M、N，各点均不重合且满足.

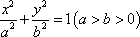
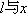
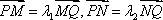
（1）求椭圆的标准方程；

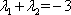
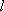
（2）若，试证明：直线过定点并求此定点.

正确答案

见解析

解析

知识点

向量在几何中的应用等差数列的性质及应用椭圆的定义及标准方程直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 14 分

设椭圆的左、右焦点分别为，点在椭圆上且在轴上方，。

（1）求椭圆C的方程；

（2）抛物线过点，连结并延长与抛物线交于点，是抛物线上一动点（且在与之间运动），求面积的最大值。

正确答案

见解析。

解析

知识点

余弦定理椭圆的定义及标准方程直线、圆及圆锥曲线的交汇问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 直线、圆及圆锥曲线的交汇问题

扫码查看完整答案与解析