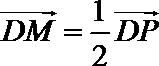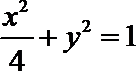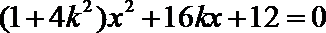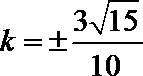- 直线、圆及圆锥曲线的交汇问题
- 共263题
21.已知圆



(1)求椭圆的方程;
(2)过椭圆外一点








正确答案
(1)






(2)设直线



可得:
设

则
化简得:
可得:

解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆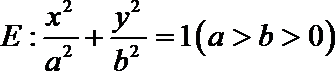
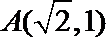

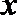
(Ⅰ)求椭圆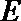
(Ⅱ)过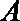

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知左焦点为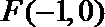

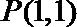
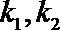
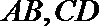
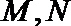
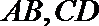
(1)求椭圆的标准方程;
(2)若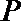
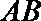
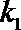
(3)若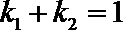
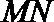
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆
(1)求椭圆E的方程;
(2)若M,N是直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知双曲线



(Ⅰ)如果椭圆

(Ⅱ)如果椭圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知点




(Ⅰ)试判断点

(Ⅱ)是否存在过




正确答案
(Ⅰ)因点


所以点




(Ⅱ)解法一:假设存在满足题设的直线



依题意,得
①当直线
②当直线


联立方程组
消去

∴

此时,方程(*)为
∴存在满足题设的直线
且直线


解法二:假设存在满足题设的直线



依题意,得
易判断直线

∴设直线

联立方程组
消去

∵
∴直线与轨迹
又

∴存在满足题设的直线
且直线


解法三:假设存在满足题设的直线



依题意,得
∵

∴有


当


∴


注意到点



∴存在满足题设的直线
且直线


解析
解析已在路上飞奔,马上就到!
知识点
23.给定椭圆






(1)求椭圆
(2)点






①当


②求证:
正确答案
(1)
所以,椭圆方程:
准圆方程:
(2)①易知
设直线为
联立
因为椭圆与直线有且只有一个交点,
所以
所以
②<ⅰ>当

设直线
由
同理,联立

由(*)(**)可知,


因此
<ⅱ>当

所以
解析
解析已在路上飞奔,马上就到!
知识点
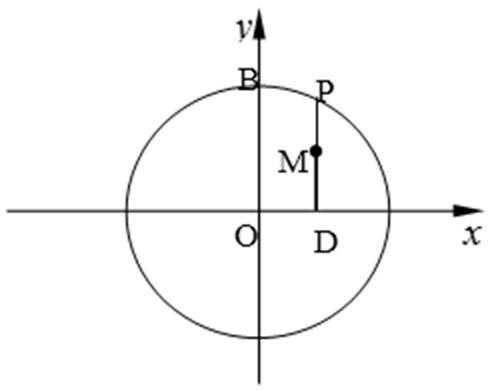
21.如图,圆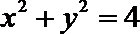
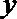
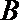
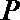

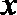
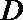
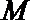
(1)求动点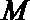
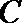
(2)过点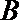
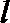

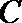
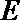
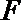

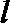
正确答案
(1)设
则由题意得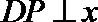
所以
又P在圆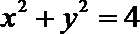
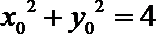
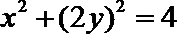
轨迹是以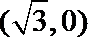
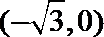
长轴长为4的椭圆。
(2)方法一:当直线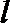
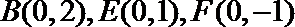
设直线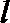
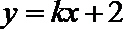
代入椭圆方程得:
△
设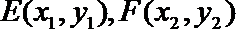
则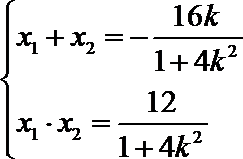
由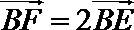
所以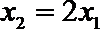
由(*)、(**)
解得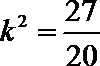
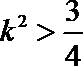
所以
即所求直线方程为: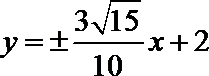
解析
解析已在路上飞奔,马上就到!
知识点
10. 函数的图象与方程的曲线有着密切的联系,如把抛物线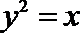
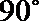
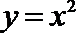
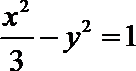
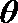
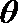
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
(1)求椭圆的方程;
(2)在线段OF上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析