- 圆的方程
- 共277题
如图,点A在直径为15的⊙O 上,PBC是过点O的割线,且PA=10,PB=5.。
(1)求证:PA与⊙O相切;
(2)求SACB的值。
正确答案
见解析
解析
(1)证明:连结OA,因为⊙O的直径为15,所以OA=OB=7.5
又PA=10,PB=5,所以PO=12.5………………………2分
在△APO中,PO2=156.25,PA2+OA2=156.25
即PO2= PA2+OA2,所以PA⊥OA,又点A在⊙O上
故PA与⊙O相切………………………5分
(2)解:∵PA为⊙O的切线,∴∠ACB=∠PAB,
又由∠P=∠P, ∴△PAB∽△PCA,∴
设AB=k,AC=2k, ∵BC为⊙O的直径且BC=15 ,AB⊥AC
∴
∴
知识点
如图,已知







(1)求证:
(2)若

正确答案
见解析
解析
解析:(1)如图,连结


又
因此
(2)连结

又




知识点
在极坐标系中,圆


(1)求圆C的标准方程和直线
(2)若直线

正确答案
见解析
解析
(1)由
所以直线

由
又
所以,圆

(2)因为直线


两边平方得
所以a的取值范围是
知识点
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线l的参数方程为

(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当α变化时,求|AB|的最小值。
正确答案
见解析
解析
(1)由
所以曲线C的直角坐标方程为
(2)将直线l的参数方程代入
设A、B两点对应的参数分别为t1、t2,则
t1+t2=

∴|AB|=|t1-t2|==
当α=时,|AB|的最小值为4
知识点
设动点





(1)求点
(2)设圆








(3)过



正确答案
见解析
解析
解析:(1) 由题意知,所求动点



(2) 设圆心
圆的方程为
令

即弦长
(3)设过F的直线方程为
由

由韦达定理得
同理得
四边形

知识点
已知圆









(1)写出圆
(2)求
正确答案
(1)
解析
解析:(1)圆

转化成直角坐标方程为

(2)由点

将直线




设

所以

知识点
在直角坐标系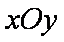
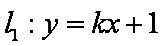
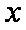
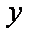
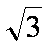
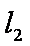
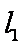
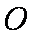
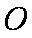
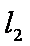
(1)求圆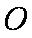
(2)圆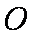
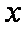
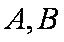
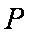
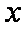

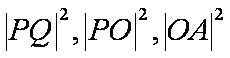
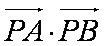
正确答案
见解析
解析
(1)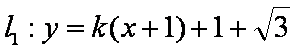
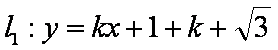
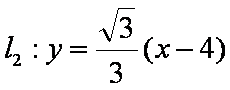
由圆O与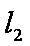
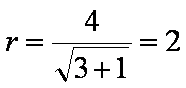
(2)不妨设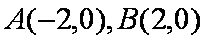
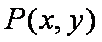
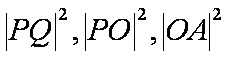
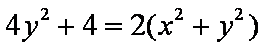
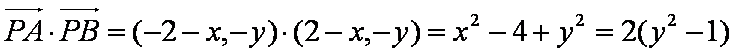
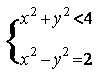
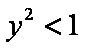
知识点
椭圆





(1)求椭圆
(2)若椭圆上两点


正确答案
见解析
解析
(1) 
将点


所以椭圆

(2)法一:设点
则

由
所以直线

法二:设点
设直线

将
得
由

所以直线

知识点
如图,三棱台ABC﹣DEF中,CF⊥平面DEF,AB⊥BC。
(1)设平面AEC∩平面DEF=a,求证DF∥a;
(2)若EF=CF=2BC,试同在线段BE上是杏存在点G,使得平面DFG⊥平面CDE,若存在,请确定G点的位置;若不存在,说明理由。
正确答案
见解析。
解析
(1)证明:在三棱台ABC﹣DEF中,AC∥DF,
∵AC⊂平面ACE,DF⊄平面ACE,
∴DF∥平面ACE,
∵DF⊂平面DEF,平面ACE∩平面DEF=a,
∴DF∥a。
(2)线段BE上存在点G,且BG=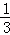
证明如下:
取CE中点O,连结FO并延长交BE于点G,连结GD、GF,
∵CF=EF,∴GF⊥CE,
在三棱锥ABC﹣DEF中,AB⊥BC,∴DE⊥EF,
由CF⊥平面DEF,得CF⊥DE,又CF∩EF=F,
∴DE⊥平面DEF,∴DE⊥GF,
∵GF⊥CE,GF⊥DE,CE∩DE=E,∴GF⊥平面CDE,
又GF⊂平面DFG,∴平面DFG⊥平面CDE,
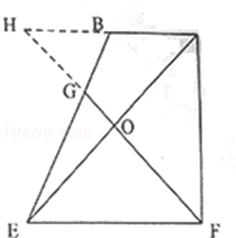
此时,如平面图所示,∵O为CE中点,CF=EF=2BC,
由平面几何知识,得△HOC≌△FOE,
∴HB=BC=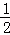
由△HGB∽△FOE,得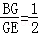
∴BG=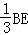
知识点
已知点


















正确答案

解析
解析:
设




将



知识点
扫码查看完整答案与解析