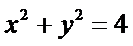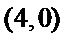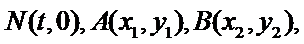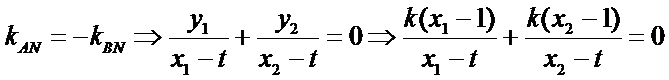- 圆的方程
- 共277题
15.设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若
正确答案
知识点
20.已知椭圆


(I)求椭圆
(II)设直线与椭圆






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若圆
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
22.已知焦点为





(Ⅰ)求
(Ⅱ)若



正确答案
解:
(1)

联立直线方程,化简为
设A(





当K不存在时,

综上,
(2)
由韦达定理知 

当
当



解析
解析已在路上飞奔,马上就到!
知识点
19. 已知椭圆E:
(1)求圆C的方程;
(2)若直线FG与直线l交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在定点P, 使得
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.能把圆x2+y2=8的周长和面积同时分为相等的两部分的函数称“周易函数”,下列函数:
①f(x)=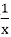
②f(x)= 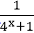

③f(x)=sin 2x;
④y=tan(x+
是周易函数的是( )
正确答案
解析
由定义可知周易函数的图象经过圆心,且是奇函数.
①不是,f(x)=
②是,因为f(-x)= 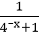

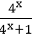

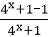



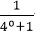

③也是;
④不是,因为y=tan(x+
综上所述,是周易函数的是②③,故选B.
知识点
15.已知圆 C : (x —3)2 + (y — 4) 2= 1 和两点 A (-m,0),B(m,0) (m>0),若圆上存在点 P,使得 ∠APB = 90°,则m的取值范围是 .
正确答案
[4,6]
解析
圆心C(3,4),半径r=1,AP垂直BP,所以(a+m)(a-m)+b2=0,即m2=a2+b2,所以OP的最大值为OC+r=5+1=6,最小值为4,所以填[4,6].
考查方向
圆的方程,两点间距离公式,最值问题。
解题思路
利用向量垂直时的数量积关系,将m转换成求OP的最大值
易错点
找不到m在圆中所代表的含义,不会运用转换思想。
知识点
2. 已知两点

正确答案
解析
圆心为OA中点,坐标为(-1,0),直径为
考查方向
解题思路
圆心坐标为OA中点(-1,0),半径为OA长度的一半,然后直接得到圆的方程。
易错点
找错圆心或半径
知识点
20.已知直线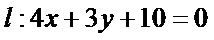
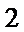
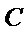
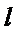
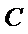
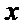
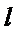
(Ⅰ)求圆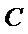
(Ⅱ)过点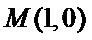
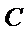
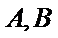
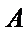
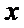
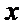
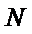
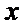
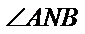
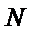
正确答案
(Ⅰ)
(Ⅱ)存在N
解析
试题分析:本题是直线与圆的位置关系的常见题型,运算量较大。此类问题往往要用到韦达定理,设而不求等方法技巧,把几何关系转化为代数运算。
(Ⅰ)设圆心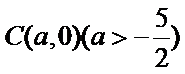
则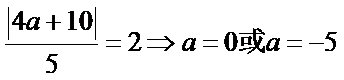
所以圆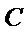
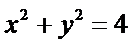
(Ⅱ)当直线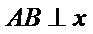
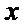
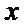
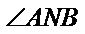
当直线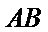
设直线
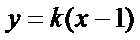
联立圆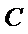
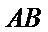
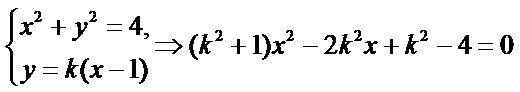
故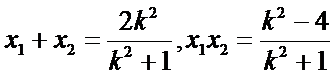
若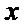
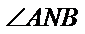
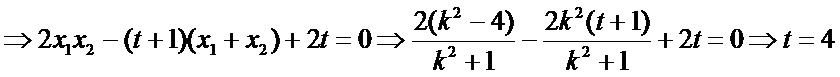
当点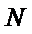
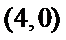
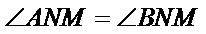
考查方向
解题思路
本题主要考查圆的标准方程、直线与圆的位置关系、点到直线的距离公式等基础知识,
解题步骤如下:根据直线与圆相切的定义,求出圆方程;由直线与圆的位置关系,建立方程组,结合韦达定理,和斜率关系,得出结果。
易错点
第一问易忽视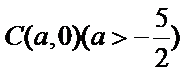
第二问不能理解“若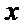
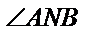
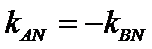
知识点
15.已知圆 C : (x —3)2 + (y — 4) 2= 1 和两点 A (-m,0),B(m,0) (m>0),若圆上存在点 P,使得 ∠APB = 90°,则m的取值范围是 .
正确答案
[4,6]
解析
圆心C(3,4),半径r=1,AP垂直BP,所以(a+m)(a-m)+b2=0,即m2=a2+b2,所以OP的最大值为OC+r=5+1=6,最小值为4,所以填[4,6].
考查方向
圆的方程,两点间距离公式,最值问题。
解题思路
利用向量垂直时的数量积关系,将m转换成求OP的最大值
易错点
找不到m在圆中所代表的含义,不会运用转换思想。
知识点
扫码查看完整答案与解析