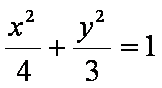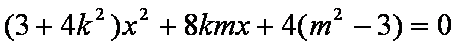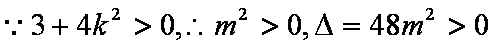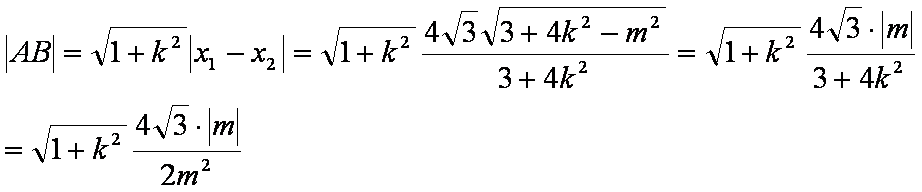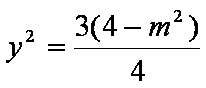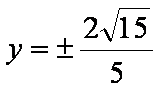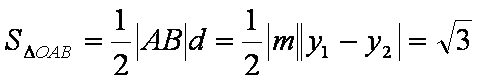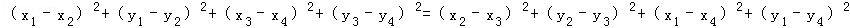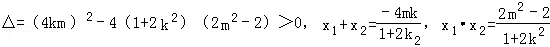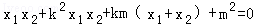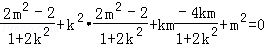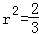- 椭圆的定义及标准方程
- 共573题
在直角坐标系












(1)求椭圆
(2)设点








正确答案
见解析
解析
解析:(1)由


∵



得:







消去



故椭圆方程为
(2)设


则





由



以

整理得:
解


∴ 以

知识点
已知直线l:y=x+



(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证两切线斜率之积为定值。
正确答案
见解析
解析
(1)解:设椭圆半焦距为c,圆心O到l的距离d=

∴直线l被圆O截得的弦长为
由2b=

∵椭圆E:


∴
∴
∴椭圆E的方程为
(2)证明:设P(x0,y0),过点P的椭圆E的切线l0的方程为y﹣y0=k(x﹣x0)
与椭圆方程联立,消去y可得(3+2k2)x2+4k(y0﹣kx0)x+2(kx0﹣y0)2﹣6=0
∴△=[4k(y0﹣kx0)]2﹣4(3+2k2)[2(kx0﹣y0)2﹣6]=0
∴(

设满足题意的椭圆的两条切线的斜率分别为k1,k2,
∴k1k2=﹣
∵P在圆O上,∴
∴k1k2=﹣
∴两切线斜率之积为定值﹣1。
知识点
在平面直角坐标系







(1)求椭圆C的方程;
(2)设P为椭圆上一点,且满足


正确答案
见解析
解析
解析:(1)∵

则椭圆方程为
设
当

解得


(2)设
由

由


∴

由点P在椭圆上,得

又由




则

由①,得
联立②,解得


知识点
如图,设椭圆











(1)求椭圆
(2)过点












正确答案
见解析
解析
解析:
(1)解:设椭圆的半焦距为




得




所以椭圆
(2)证明:若直线






于是
若直线

由







设


与椭圆

得

于是
综上得
知识点
已知椭圆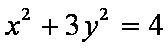
(1)求证:BC恒过轴上一定点;
(2)求△ABC面积的最大值;
正确答案
见解析。
解析
(1)显然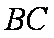
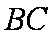
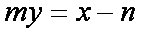
与椭圆联立得: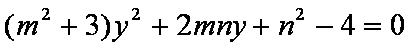
设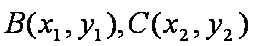
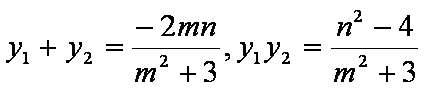
因为
所以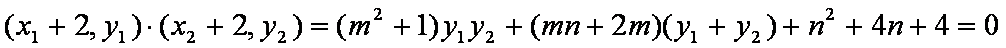
①带入②化简可得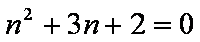
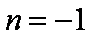
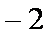
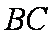
(2)

设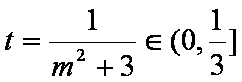
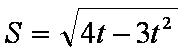
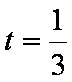
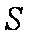
即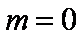
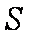
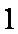
知识点
已知随机变量


正确答案
解析
知识点
已知椭圆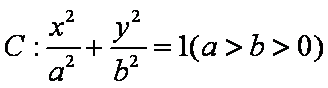
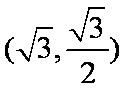
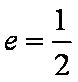
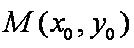
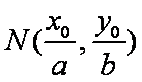
(1)求椭圆C的方程;
(2)若椭圆C的右顶点为D,上顶点为E,试探究ΔOAB的面积与ΔODE的面积的大小关系,并证明。
正确答案
见解析
解析
(1)由已知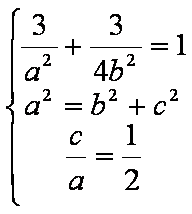
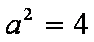
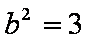
(2)设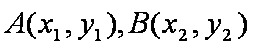
(i)当直线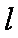
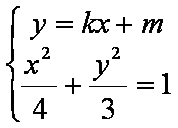
有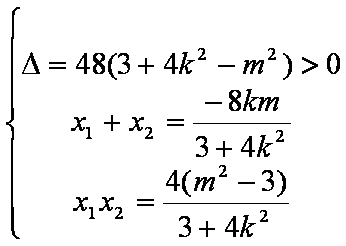
由以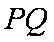
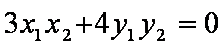
整理得: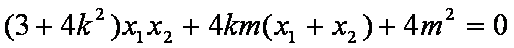
将①式代入②式得: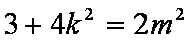
又点
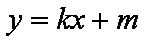
所以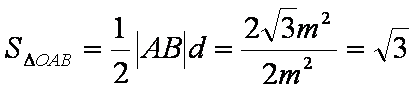
(ii)当直线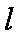
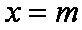
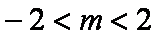
联立椭圆方程得:
代入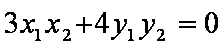
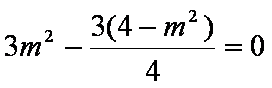
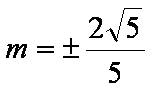
综上: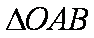
又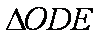
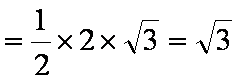
知识点
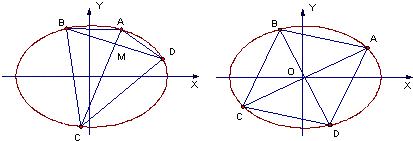
如图,已知椭圆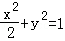
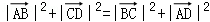
(1)证明:AC⊥BD;
(2)若M点恰好为椭圆中心O
(i)四边形ABCD是否存在内切圆?若存在,求其内切圆方程;若不存在,请说明理由。
(ii)求弦AB长的最小值。
正确答案
见解析
解析
(1)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)
由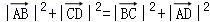
展开整理得:x1x2+y1y2+x3x4+y3y4=x2x3+y2y3+x1x4+y1y4
即x1(x2﹣x4)+x3(x4﹣x2)+y1(y2﹣y4)+y3(y4﹣y2)=0
∴(x1﹣x3)(x2﹣x4)+(y1﹣y3)(y2﹣y4)=0
即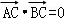
∴ AC⊥BD…,(4分)
(2)解:(i)∵AC⊥BD,由椭圆对称性知AC与BD互相平分,
∴ 四边形ABCD是菱形,它存在内切圆,圆心为O,设半径为r,直线AB方程为:y=kx+m
则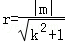
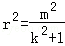
联立 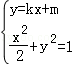
∴
由(1)知OA⊥OB,
∴ x1x2+y1y2=0,即x1x2+(kx1+m)(kx2+m)=0
∴
∴
∴ 2m2﹣2+2m2k2﹣2k2﹣4k2m2+m2+2m2k2=0
∴ 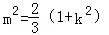
②代入①有:
∴ 存在内切圆,其方程为: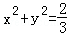
容易验证,当k不存在时,上述结论仍成立。
(ii)
∵
∴ 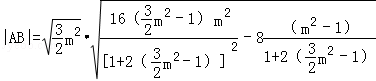
令3m2﹣1=t,则
∴
∵ 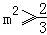
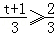
当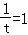
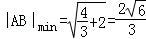
容易验证,当k不存在时,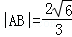
知识点
设






(1)求
(2) 设点


正确答案
见解析
解析
解析:(1)由椭圆定义知

得



设

化简的
则
因为直线AB斜率为1,所以
得
所以E的离心率
(2)设AB的中点为


由

即
得
故椭圆E的方程为
知识点
已知圆



(1)求椭圆
(2)若存在直线










正确答案
见解析
解析
解:(1)设椭圆的焦距为2c,因为
所以椭圆的方程为
(2)设
联立方程得
所以
则
又点


显然,若点




当

当

又显然

综上,圆


知识点
扫码查看完整答案与解析