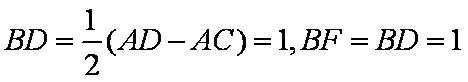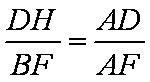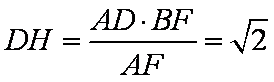- 椭圆的定义及标准方程
- 共573题
已知椭圆E:
原点对称的两点,且直线PA的斜率与直线QA的斜率之积为
(1)求E的方程;
(2)过E的右焦点作直线与E交于M、N两点,直线MA、NA与直线
分别交于C、D两点,设△ACD与△AMN的面积分别记为


正确答案
见解析
解析
(1)设

又
故
(2)设直线


设
直线MA的方程为

同理
所以
所以



所以
记

所以


故
知识点
已知椭圆E:





(1)求椭圆E的方程;
(2)若点A与椭圆上的另一点C(非右顶点)关于直线l对称,直线l上一点N(0,y0)满足

正确答案
见解析。
解析
(1)由题意,A(﹣a,0),B(0,b),F(1,0),
∵



∴b2﹣a﹣1=0,
∵b2=a2﹣1,∴a2﹣a﹣2=0,解得a=2,
∴a2=4,b2=3,
∴椭圆E的方程为
(2)设C(x1,y1)(y1≠0),且A(﹣2,0),则AC的中点M(

由已知kAC=

∴l:y﹣


令x=0,则y0=

即N(0,﹣
∴




∴7x12+96x1﹣28=0
∴x1=
∴y1=±
∴C(

知识点
已知椭圆


(1)求椭圆
(2)若



试确定
正确答案
见解析。
解析
(1)由已知,


由




∴

(2)①若直线





②若直线


由

∴
∴
∵


综上,

知识点
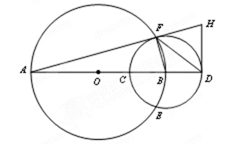
如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O
于E、F两点,过点D作垂直于AD的直线,交直线AF于点H。
(1)求证:B、D、H、F四点共圆;
(2)若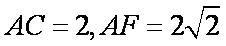
正确答案
见解析
解析
(1)因为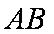
又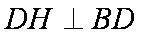
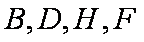
(2)因为AH与圆B相切于点F,
由切割线定理得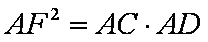
所以
又△AFB∽△ADH,所以
由此得
连接BH,由(1)知,BH为△BDF外接
故△BDF的外接圆半径为
知识点
如图,在平面直角坐标系





(1)若


(2)若
(3)求证:以


正确答案
见解析
解析
(1)因为



由


又
所以


(2)当

由



所以

(3)依题意,椭圆右焦点到直线


由


由①②得,
解得

所以

所以以


知识点
极坐标系中椭圆C的方程为 

(1)求该椭圆的直角标方程,若椭圆上任一点坐标为

(2)若椭圆的两条弦




正确答案
见解析。
解析
(1)该椭圆的直角标方程为
设
所以

(2)设直线



则直线


代入
即
设


同理
所以
知识点
在平面直角坐标系


(1)求椭圆C的方程;
(2)设P为椭圆上一点,且满足

正确答案
(1)
解析
解析:(1)∵

则椭圆方程为
设
当

解得


(2)设
由

由


∴

由点P在椭圆上,得

又由




则

由①,得
联立②,解得


知识点
如图,已知椭圆



(1)求此椭圆的标准方程;
(2)设P此椭圆上异于A,B的任意一点, 






正确答案
见解析
解析
解析:(1)可知,




得
椭圆方程为
(2)设
由

所以直线AQ的方程为
由

由
又因为
所以
所以直线NQ的方程为
化简整理得到
所以点O直线NQ的距离
直线

知识点
设椭圆




正确答案
答案:
解析
由





知识点
已知双曲线


正确答案
解析
由题可知,双曲线渐近线的倾角为





知识点
扫码查看完整答案与解析