- 分段函数模型
- 共10题
14.设函数
①若a=0,则f(x)的最大值为____________________;
②若f(x)无最大值,则实数a的取值范围是_________________。
正确答案
2,a<-1
知识点
10.已知函数


正确答案
解析
函数f(x)的定义域为:
关于原点对称,因为x>0时,-x<0,f(-x)=-lnx+x=f(x)
同理可知,当x<0时,f(-x)=f(x),所以f(x)为偶函数
所以f(x)在
所以当m>0时,由



所以此题选B
考查方向
分段函数的性质,偶函数的性质,函数的单调性
解题思路
先求出定义域,然后判断函数的单调性和奇偶性
然后根据奇偶性的性质,求出参数的取值范围
易错点
讨论函数性质时错误,判断函数奇偶性错误
教师点评
分段函数多涉及到分类讨论,学生在解题时要充分注意到
知识点
18.通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设


(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
正确答案
(1)当





(2)
(3)当



当
当

综上,学生注意力在180以上所持续的时间28.57-4=24.57>24,所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题。
解析
解析已在路上飞奔,马上就到!
知识点
19.某工厂生产某种产品,每日的成本C(单位:元)与日产里



已知每日的利润


(Ⅰ)求
(Ⅱ)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
解:(Ⅰ)由题意可得:
解析
解析已在路上飞奔,马上就到!
知识点
20.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。(注:年利润一年销售收入一年总成本)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?
(注:年利润=年销售收入—年总成本)
正确答案
解:(1)当

(2)①当
②当
综合①②知当
解析
解析已在路上飞奔,马上就到!
知识点
21.某商场在国庆促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案相应获得第二次优惠(获得奖券):
根据上述促销方法,顾客在该商场购物可以获得双重优惠。例如:购买标价为600元的商品,则消费金额为480元,480∈[400,500),所以获得第二次优惠金额为60元,获得的优惠总额为:600×0.2+60=180(元)。
设购买商品的优惠率=
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
正确答案
(1)标价为1000元的商品消费金额为800元,获得奖券150元,优惠额为350元,所以优惠率为0.35
(2)y=
(3)购买标价在[625,800)(元)内的商品,消费金额在[500,640)(元)内。
设顾客购买标价为x元的商品,(625≤x<800),消费金额为0.8x.获得奖券100元,此时优惠率为
综上所述,顾客购买标价的取值范围为[625,750](元)时,可得到不小于
解析
解析已在路上飞奔,马上就到!
知识点
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放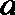
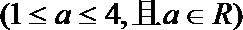
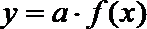
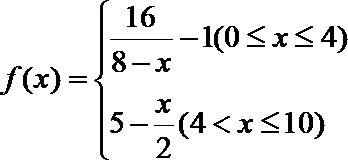
(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放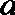
正确答案
(1)因为 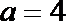
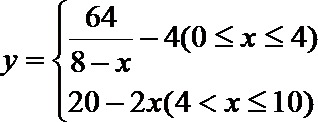
①当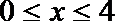
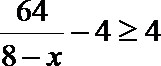
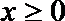
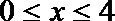
②当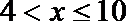
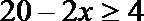
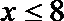
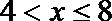
综合得,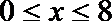
(2) 当
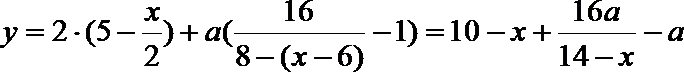
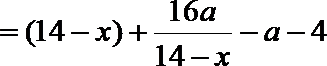
由题意知,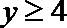
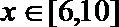
因为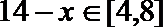
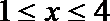
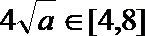
故当且仅当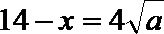
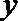

令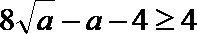
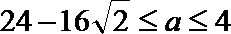
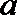
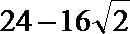
又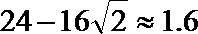
解析
解析已在路上飞奔,马上就到!
知识点
17.为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度




(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知f(x)=
正确答案
解析
∵ 当x≤1时,f(x)=(4﹣


知识点
扫码查看完整答案与解析


































